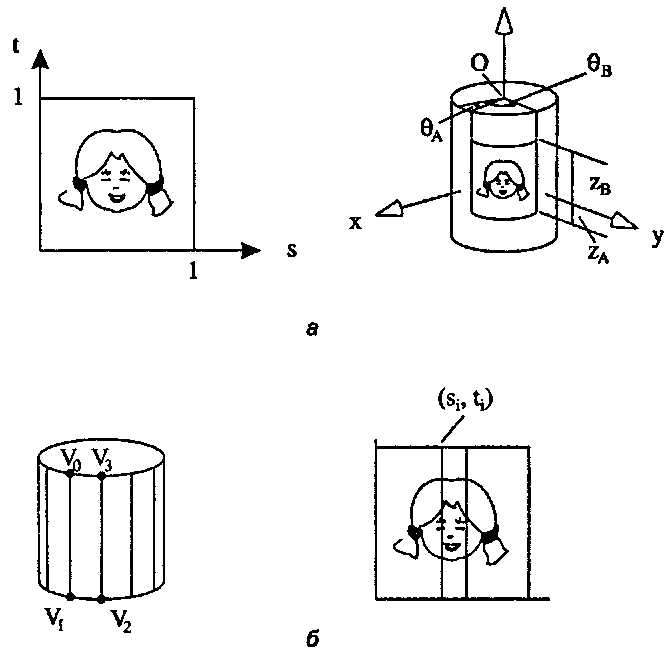
Рис. 8.50. Обертывание этикетки вокруг цилиндра
8.5. Добавление текстуры к граням Геометрия достаточно проста, и решение не вызывает затруднений. Существует прямая линейная зависимость между текстурными координатами (х, £) и парой азимут-высота (8, г) для точки на поверхности цилиндра"images/tmp8E4A-578.png">
Таким образом, если боковая поверхность цилиндра состоит из N граней, то левое ребро г'-й грани имеет азимут 0 = -, а текстурные координаты его верхней левой вершины равны N
Аналогично находятся текстурные координаты и остальных трех вершин грани. Связь между координатами (х, г) и вершинами каждой грани нетрудно включить в цикл подпрограммы моделирования (см. упражнения в конце раздела).
Сложнее обстоят дела в тех случаях, когда объект не является простым цилиндром. Ниже мы увидим, как отображать текстуру на поверхности вращения более общего вида.
Пример 8.5.2. «Обертывание со сжатием» этикетки вокруг поверхности вращения Напомним из главы 6, что поверхность вращения задается с помощью профильной кривой (х(р), 2(и)),' как показано на рис. 8.51, а, и имеет следующую параметрическую форму: Р(и, ю) - (х(ю)со5и,х(и)5'ти, г(р)). Форма - в данном случае это ваза - смоделирована в виде совокупности граней, стороны которых располагаются вдоль контуров с постоянными и и о (рис. 8.51, б).
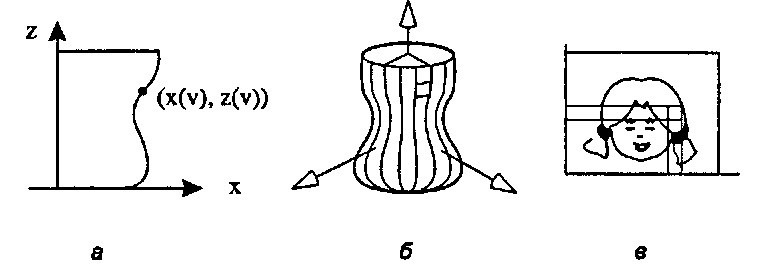
Рис 8.51. Обертывание этикетки вокруг вазы: а) профиль вазы; б) грань вазы; в) четыре угла Тогда заданная поверхность F имеет четыре вершины: P(ut, v), Р(и{+1, vt), P(ut, vl+l), P(uiH, vi+i). Требуется найти для каждой из этих вершин соответствующие координаты (s t).
Естественно было бы поступать так же, как раньше, и считать s и v линейно зависящими от и и о, как в уравнении (8.22). Это эквивалентно оборачиванию текстуры вокруг воображаемого резинового цилиндра, заключающего в себе вазу (рис. 8.52, а), а затем сжатию цилиндра, вследствие чего каждая точка текстуры перемещается радиально (и горизонтально) до тех пор, пока не достигнет поверхности вазы. Такой метод называется «обертыванием со сжатием» («shrink-wrapping»), его авторами являются Бир и Слоун (Bier and Sloane - [Bier, 20]), которые изобрели несколько способов отображения текстуры на различные классы форм. Эти авторы рассматривают обертывание со сжатием в терминах воображаемого нормального вектора (рис. 8.52, б): точка текстуры Pt связана с точкой объекта Vt, расположенной на внутренней нормали к образующей цилиндра, проходящей через Рг Метод обертывания со сжатием хорошо работает для цилиндроподобных объектов, однако узор текстуры будет искажен, если профильная кривая имеет сложную форму.
