Рис. 9.8. Несколько первых поколений кривой Гильберта Практические упражнения
9.3.1. Как велик дракон?
Рассмотрим кривую дракона порядка п на базе отрезка прямой между точками (0, 0) и (1, 0). Дракон лежит внутри ограничивающего прямоугольника, размеры которого увеличиваются с ростом порядка. Какие координаты имеют углы этого прямоугольника при увеличении порядка п до бесконечности? Чему равна длина кривой дракона и-го порядка?
9.3.2. Дракон - это сложенная полоска бумаги Интересно отметить, что кривую дракона можно получить, последовательно складывая тонкий лист бумаги. Разгладьте такой лист, а затем сложите его так, чтобы один конец совместился с другим. Повторяйте этот процесс неограниченно, складывая лист в одном и том же направлении. (Реально можно проделать только около семи сложений.) Когда вы развернете бумагу так, что все углы будут равны 90°, то увидите кривую дракона. Покажите, что данный процесс действительно приводит к кривым дракона порядков от 1 до 4.
9.3.3. Что это за кривые?
С помощью нижеприведенных инструкций определяются еще две кривые. Первая из них является вариантом замкнутой кривой Серпинского, а вторая - прототипом кривой Пеано [Wagon, 204]. Нарисуйте первые три поколения каждой кривой.
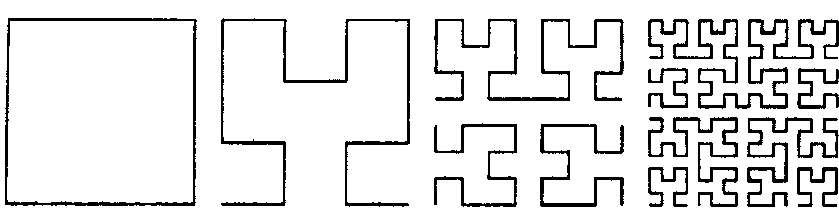
О CepnHHCKHH-6HC"images/tmp8E4A-608.png" alt="Заполняющая плоскость кривая Поля">
Рис. 9.9. Заполняющая плоскость кривая Поля
