9.5.1. Экспериментальный копир
В данном разделе снова вводятся в игру системы итерируемых функций (IFS), впервые описанные в главе 2. Берем исходный образ 70 и помещаем его в специальный «фотокопир», создающий новое изображение 7,, как показано на рис. 9.29, аК Изображение 7, является не простой копией исходного изображе1 Это описание основано на статье, написанной в 1990 году Юргенсом, Пайтгеном и Саулом (Jürgens, Peitgen, Saupe - [Jürgens, 119]).
9.5. Создание изображений с использованием системы итерируемых функций ния 70, а, как мы скоро увидим, совмещением нескольких уменьшенных версий 70. Затем берем изображение /( и посылаем его обратно в копир, чтобы получить следующее изображение 12. Повторяя этот
процесс бесконечно, получим последовательность изображений /0, 12.....которая называется орбитой
I0 (orbit of /0). (Вспомните орбиту в главе 2.) Зададимся вопросом: «сходятся» ли эти изображения к какому-нибудь изображению и если да, то к какому?
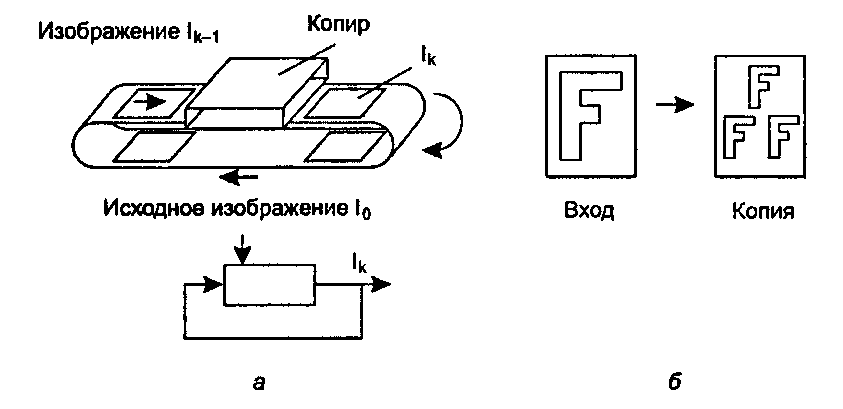
Рис. 9.29. Создание новых «копий» из старых
Пример 9.5.1. «Копир Серпинского» Рассмотрим особый пример копира, который можно назвать суперкопиром, или «Б-копиром». Он вкладывает друг в друга три уменьшенных версии любого изображения, которое подается на его вход. На рис. 9.29, б показано, что делает Б-копир за один проход, если на вход подана буква Е Эти три уменьшенных изображения могут быть с тем же успехом совмещены, хотя на рисунке этого не показано. На рис. 9.30 приведено несколько первых «итераций», которые производит Б-копир. Из рисунка видно, что эти итерации сходятся к треугольнику Серпинского, который уже встречался нам ранее, и на самом деле это так! При каждой итерации отдельный компонент ^ становится вдвое меньше, а количество компонентов утраивается. По мере увеличения числа итераций размер букв Е приближается к точке, и эти точки выстраиваются в треугольник Серпинского. «Окончательное» изображение не зависит от формы буквы Е, а только от свойств самого суперкопира.
