На рис. 9.41 показано несколько примеров орбит для различных значений константы с, наложенных на схематическое изображение множества Мандельброта, приведенное для ориентации. Каждая орбита показана в виде ломаной линии, начинающейся в соответствующем ей значении с, показанном точкой на графике. (Мы могли бы нарисовать каждую орбиту с началом в точке 0, однако это загромоздило бы график.) Обратите особое внимание на то, что каждая точка показывает соответствующее значение с, используемое в итерационной системе/(.) = (.)2 + с, а также стартовую точку орбиты.
Если значение с выбрано вне множества М, то полученная орбита взрывается. На рисунке показаны четыре взрывающиеся орбиты. Если значение с выбрано вне границ множества М, то орбита обычно
9.6. Множество Мандельброта дико мечется по плоскости и наконец уносится в бесконечность. Такие орбиты затруднили бы понимание картины и поэтому на рисунке не показаны. В тематическом задании 9.4 в конце главы приводится скелет программы, рисующей орбиты для произвольных значений с. Это тематическое задание является отличной тренировкой для развития интуиции относительно итераций функции (.)2 + с.
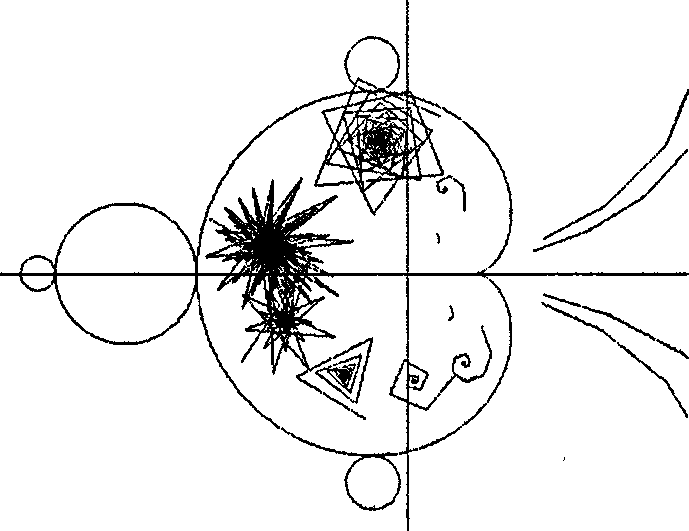
Рис. 9.41. Примеры орбит на плоскости с
Если же значение с выбрано внутри множества М, то соответствующая орбита Может вести себя по-разному. Для некоторых значений с она сразу втягивается в неподвижную точку, для других - движется к этой точке по спирали (очень медленно, если с находится вблизи границы М).
Для того чтобы понять возможное поведение орбиты, полезно представить, что каждое значение с определяет две неподвижные точки в соответствии с уравнением (9.15). Если одна из них является точкой притяжения (это так, если она лежит внутри круга радиуса 1/2 с центром в начале координат), то нулевая орбита сразу втягивается в эту точку. Несколько примеров таких орбит показано на рис. 9.41. (Отметим, что точка с не то же самое, что неподвижная точка.) С другой стороны, если ни одна неподвижная точка не является точкой притяжения, то орбита не будет сходиться ни к какому определенному значению. Вместо этого она будет втянута в некоторую циклическую последовательность значений, которая «крутится» вокруг одной из неподвижных точек отталкивания. К примеру, орбиты для значений с, лежащих в маленьких кругах в верхней и нижней частях множества М, имеют период, равный трем.
