11.4. Применение кривых Безье для построения кривых
При изменении £ относительные веса этих четырех векторов тоже изменяются, вследствие чего вектор р(г) смещается на различные позиции. Попробуйте выяснить, какие веса будут иметь векторы при г - 0,5 и какую долю внесет каждый из них в формирование результирующего вектора р(0,5).
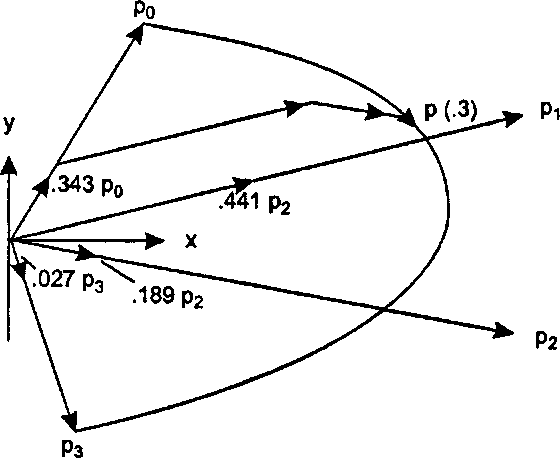
Рис. 11.15. Сопряжение четырех векторов с помощью полиномов Бернштейна Обобщение алгоритма де Кастельо на произвольное число точек Мы уже видели, что в алгоритме де Кастельо для создания квадратичных параметрических представлений используется твининг по трем точкам, а для кубических представлений - по четырем точкам. Данный алгоритм можно легко обобщить на случай использования (Ь + 1) контрольной точки"images/tmp8E4A-754.png">
Читатели, знакомые с теорией вероятностей, отметят сильное сходство между этим выражением и биномиальным распределением вероятностей.
В отечественной литературе для биномиальных коэффициентов чаще используется обозначение Скь. - Примеч. пер.
23 Ф. Хилл
Создание кривых и поверхностей
При L < k значение этого коэффициента равно нулю. Из равенства (11.26) видно, что каждый из полиномов Бернштейна имеет степень L. Как и прежде, полиномы Бернштейна совпадают с членами разложения выражения [(1 - г) + f]V поэтому мы можем быть уверены, что для всех t
£#(o=i (iL28>и что P(t) является полноправным аффинным преобразованием точек.
Практические упражнения
11.4.1. Создание кривой вручную
Используя метод де Кастельо для трех точек (0,0), (2,4), (6,1), постройте на миллиметровке кривую P(t) для следующих значений: t = 0, 0,2, 0,4, 0,6, 0,8,1,0.
