11.6.1. Проблема локального контроля Еще более серьезная проблема, чем относительная негибкость кривых Безье, заключается в том, что они не предоставляют достаточного локального контроля (local control) над формой кривой. На рис. 11.19 показана ситуация, в которой для создания кривой Безье (сплошная линия) используется пять контрольных точек, причем эта кривая несколько отходит от желаемой кривой (пунктир) в окрестности г = 1. Для коррекции этого отклонения пользователь смещает точки Р2 и Р3 вверх, чтобы заставить кривую Безье подойти ближе к желаемой кривой. Однако, как показано на рисунке, это также оказывает воздействие на первую половину кривой, уводя ее в сторону от желаемой кривой.

а б Рис. 11.19. Редактирование участков кривой Проблема заключается в том, что изменение любой контрольной точки изменяет всю кривую. Эта взаимосвязь вытекает из природы полиномов Бернштейна (вспомним рис. 11.14): каждый из них «активен» (в смысле отличен от нуля) на всем интервале [0,1]. Тот интервал, в котором функция отлична от нуля, часто называют ее поддержкой (support). Поскольку каждый полином Бернштейна поддерживается во всем интервале [0,1] и поскольку кривая Безье является объединением этих функций, то из
11.6. Нахождение лучших стыковочных функций этого следует, что каждая контрольная точка оказывает влияние на кривую для всех значений г от 0 до 1. Следовательно, изменение любой контрольной точки оказывает влияние на форму кривой повсюду, без возможности локального контроля.
Решим эту проблему с помощью более подходящего набора стыковочных функций (blending functions), приведенных на рис. 11.20. На рисунке показаны шесть стыковочных функций R0(t), R^t),…, R5(t), (которые должны быть найдены),1 имеющих поддержку только на части интервала [0,1]. Например, поддержка функции R0(t) равна [0,0,25], а поддержка функции R3(t) - [0,25,1,0]. Фактически при каждом значении t активными являются не более трех стыковочных функций.
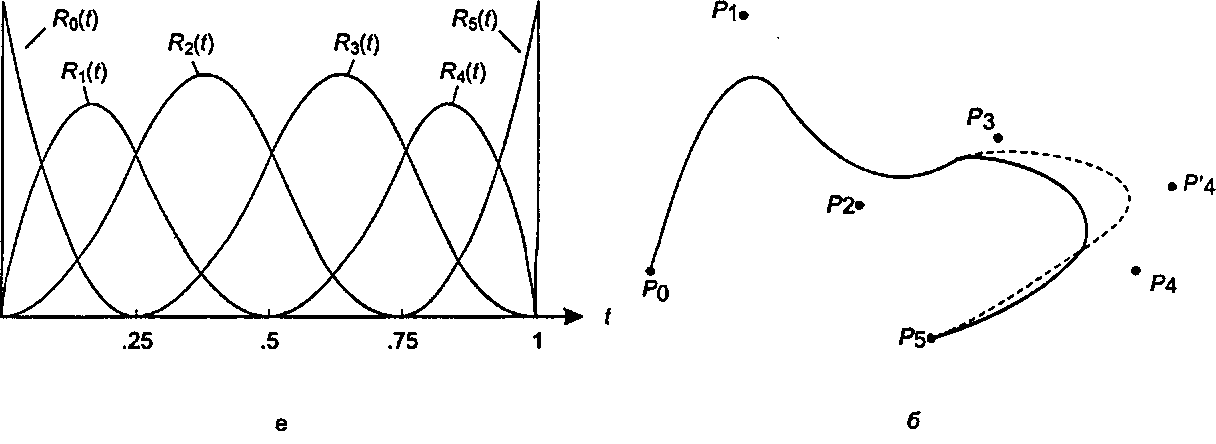
Рис. 11.20. Сопряжение функций с сосредоточенной поддержкой
