O // File circlel.cpp
void circle2 (int xc, int yc, int r, int color) {
int x = 0;

int у = r;

int d = 1 - r;
int deltal = 3;
int delta2 =-2*r + 5;
xCenter = xc; yCenter = yc;

Компьютерная графика. Полигональные модели

circlePoints ( x, у, color);

while ( у > x ) {

if ( d < 0 ) {
d +=delta1; delta 1 += 2; delta2 += 2; x++;
}
else
{
d += delta2; deltal += 2; delta2 += 4; x++;
y-;
}
circlePoints ( x, y, color);
}
}

6.3. Растровая развертка эллипса Уравнение эллипса с осями, параллельными координатным осям, имеет следующий вид:

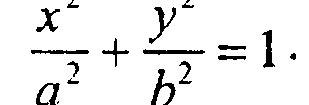
Перепишем это уравнение несколько иначе: Г(х,у) = Ь2х2 Л-а2 у2 -а2Ь2 =0. Рис. 6.6

В силу симметрии эллипса относительно координатных осей достаточно найти растровое представление только для одной из его четвертей, лежащей в первом квадранте координатной плоскости: х > 0,у > 0 .

Разобьем четверть эллипса на две части: ту, где угловой коэффициент лежит между -1 и 0, и ту, где угловой коэффициент меньше -1 (рис. 6.7).

Вектор, перпендикулярный эллипсу в точке (х, у), имеет вид

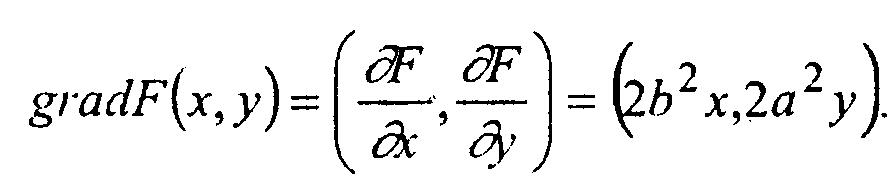
Рис. 6.7

2 2

В точке, разделяющей части 1 и 2, Ъ х = а у . Поэтому у-компонента градиента в области 1 больше л-компоненты (в области 2 - наоборот). Таким образом, если в следующей срединной точке

6. Растровые алгоритмы

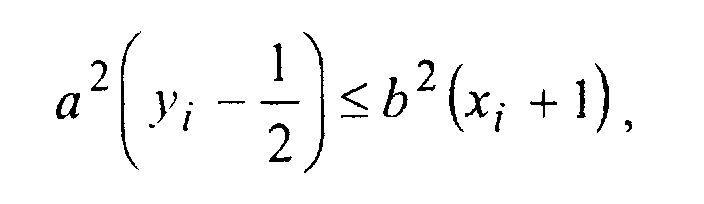
то мы переходим из области 1 в область 2.

Как и в любом алгоритме средней точки, мы вычисляем значение F между кандидатами и используем знак функции для определения того, лежит ли средняя точка внутри эллипса или вне его.

Часть 1. Если текущий пиксел равен , у^), то

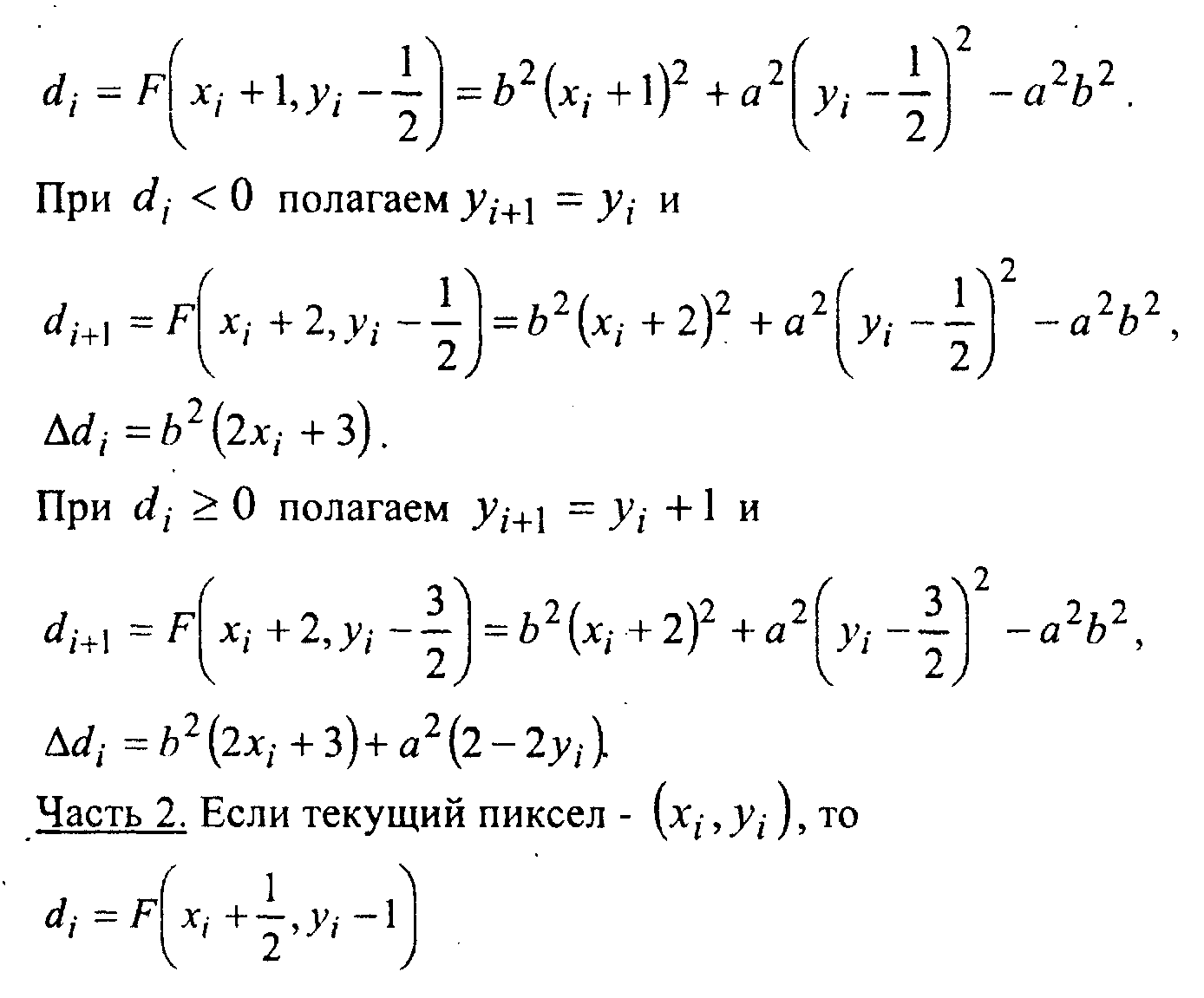
и все дальнейшие выкладки проводятся аналогично первому случаю.

Часть 2 начинается в точке (О, Ь), и (1, Ь - Уг) - первая средняя точка. Поэтому

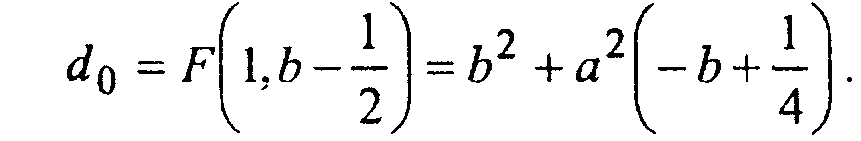
На каждой итерации в части 1 мы должны не только проверять знак переменной <//, но и, вычисляя градиент в средней точке, следить за тем, не пора ли переходить в часть 2.

6.4. Закраска области, заданной цветом границы

Рассмотрим область, ограниченную набором пикселов заданного цвета, и точку (х, у), лежащую внутри этой области.

Задача заполнения области заданным цветом в случае, когда область не является выпуклой, может оказаться довольно сложной.

⇐ Предыдущая| |Следующая ⇒