Заметим прежде всего, что особенности использования геометрических понятий, формул и фактов, как простых и хорошо известных, так и новых, более сложных, требуют особого взгляда на них и иного осмысления.
у
М (х, у)
7.1. Аффинные преобразования на плоскости В компьютерной графике все, что относится к двумерному случаю, принято обозначать символом (Ю) (2-<1ітеп5Іоп).
Допустим, что на плоскости введена прямолинейная координатная система.
Тогда каждой точке М ставится в соответствие упорядоченная пара чисел (х, у) ее координат (рис. 7.1). Вводя на плоскости еще одну прямолинейную систему координат, мы ставим в соответствие той же точке М другую пару чисел- (х*,у*).
Переход от одной прямолинейной координатной системы на плоскости к другой описывается следующими соотношениями:
*х = сое + Ву + Я,
(7.1)У ~ух + 8у + //, гДе а, р, у, Я, // - произвольные числа, связанные неравенством а р
о Рис. 7.1
У 8
*0.Замечание Формулы (7.1) можно рассматривать двояко: либо сохраняется точка и изменяется координатная система (рис. 7.2) - в этом случае произвольная точка М остается той же, изменяются лишь ее координаты
Компьютерная графика. Полигональные модели либо изменяется точка и сохраняется координатная система (рис. 7.3) -в этом случае формулы (7.1) задают отображение, переводящее произвольную точку М(х, у) в точку М*(х*, у*), координаты которой определены в той же ко ординати о й сист ем е.
о
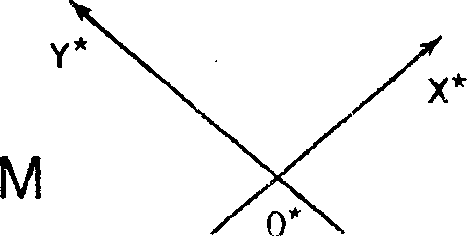
X Рис. 7.2
о
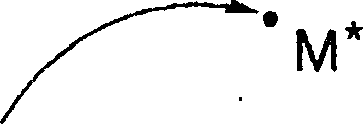
М
X Рис. 7.3
В дальнейшем мы будем рассматривать формулы (7.1) как правила, согласно которы-м в заданной системе прямолинейных координат преобразуются точки плоскости.
В аффинных преобразованиях плоскости особую роль играют несколько важных частных случаев, имеющих хорошо прослеживаемые геометрические характеристики. При исследовании геометрического смысла числовых коэффициентов в формулах (7.1) для этих случаев нам удобно считать, что заданная система координат является прямоугольной декартовой.
А. Поворот вокруг начальной точки на угол (р (рис. 7.4) описывается формулами
X - ХСО&(р- уБ1П <р, *
