I2 + С08ф(і-І2) /(і-С08ф)т + П8ІПф /(і-С08ф)ї1-тБІПф 0

/(і - со8ф)т - пБІпф т2+со8ф(і-т2) т(і-со8ф)п + /8Іпф 0

/(і - С08ф)п + ГГШПф т(і - С08ф)п -/8ІПф П2 + С08ф(і - п2) 0

0 0 0 1,
V

Рассматривая другие примеры подобного рода, мы будем получать в результате невырожденные матрицы вида

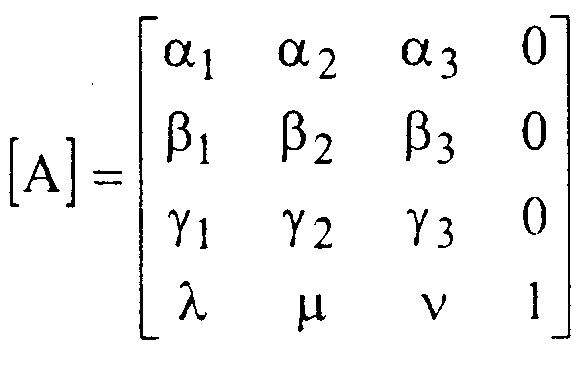
Компьютерная графика. Полигональные модели При помощи таких матриц можно преобразовывать любые плоские и пространственные фигуры.

Пример 2. Требуется подвергнуть заданному аффинному преобразованию выпуклый многогранник.

Для этого сначала по геометрическому описанию отображения находим его матрицу [А]. Замечая далее, что произвольный выпуклый многогранник однозначно задается набором всех своих вершин

Рис. 9.3

Подвергая этот набор преобразованию, описываемому найденной невырожденной матрицей четвертого порядка [И] [Л], мы получаем набор вершин нового выпуклого многогранника - образа исходного (рис. 9.3).

9.1. Платоновы тела Правильными многогранниками (Платоновыми телами) называются такие выпуклые многогранники, все грани которых суть правильные многоугольники и все многогранные углы при вершинах равны между собой.

Существует ровно 5 правильных многогранников (это доказал Евклид)"box" rules="all" border="1">

Название многогранника

Число граней - Г

Число ребер - Р

Число вершин - В

Тетраэдр

Гексаэдр

Октаэдр

Додекаэдр

Икосаэдр

Нетрудно заметить, что в каждом из пяти случаев числа Г, Р и В связаны равенством Эйлера Г + В = Р + 2.

Правильные многогранники обладают многими интересными свойствами. Здесь мы коснемся только тех свойств, которые можно применить для построения этих многогранников.

9. Преобразования в пространстве, проектирование Для полного описания правильного многогранника вследствие его выпуклости достаточно указать способ отыскания всех его вершин.

Операции построения первых трех Платоновых тел являются особенно простыми. С них и начнем.

Куб (гексаэдр) строится совсем несложно (рис. 9.4).

⇐ Предыдущая| |Следующая ⇒