Необходимо получить выражения для определения проекции вершины на плоскость экрана при центральном проецировании. Предположим, экран расположен параллельно координатной плоскости ХУ и на нем для отсчета экранных координат задана координатная система, оси которой параллельны осям мировой системы, а начало находится в точке пересечения плоскости экрана с мировой осью 2 (рис. 24.3). Линия, соединяющая центр наблюдения К и проецируемую точку пространства А пересекается с проекционной плоскостью в точке аэ. Наиболее простые выражения для координат проекции дэ в системе проекционной плоскости получаются, если дополнительно к указанным условиям центр проецирования находится в начале мировой системы координат.
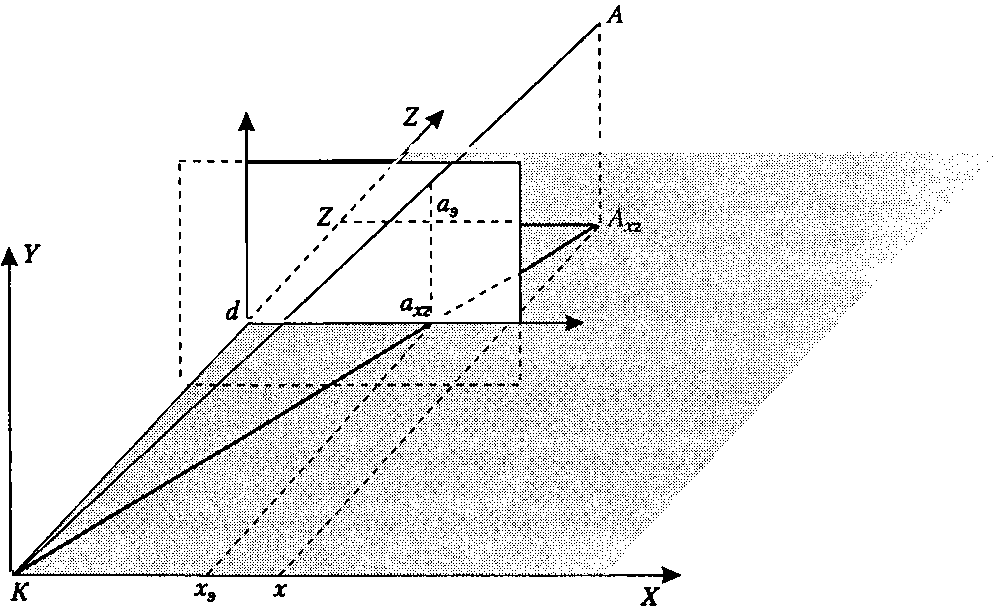
Рис. 24.3. Проецирование точки на плоскость
В этом случае абсцисса и ордината проекции в системе наблюдателя совпадают со значениями одноименных координат в проекционной плоскости.
Выражения для координаты хэ получаются из условия подобия треугольников Ксіа^ и К/і^ на плоскости Х2\
Геометрические преобразования
Из аналогичного подобия треугольников на плоскости У2 можно получить"images/tmp6745-93.png">
Однако элементы этой матрицы зависят от координаты 2 преобразуемой точки. Это значит, что нельзя вычислить одну числовую матрицу преобразования и передать ее графическому ускорителю для проецирования всех точек объекта.
Можно перейти к однородным координатам и выполнить указанное выше преобразование проецирования, используя следующее уравнение:
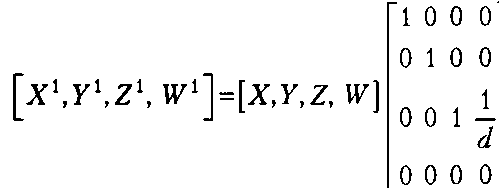
(24.7)В этом выражении матрица проецирования Рх не зависит от координат проецируемых точек, следовательно, она может быть один раз передана в аппаратный ускоритель для последующего проецирования вершин всех многогранников сцены.
Теперь нужно определить, как при вычислении данного выражения изменяются декартовы координаты. Выполнив умножение, можно получить следующие выражения:
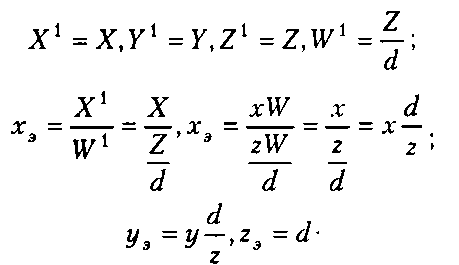
Таким образом, мы можем считать, что результатом умножения на матрицу проецирования являются точки (х.л, у:і, г0) в трехмерном пространстве, которые находятся в плоскости проецирования.
