|а v| = |ct||v|, причем при положительном а направление вектора av то же, что и направление вектора v. Обращаю ваше внимание на то, что в дальнейшем нам понадобится специальный вектор нулевой длины (нуль-вектор - zero vector), который будем обозначать полужирной цифрой 0.

Существуют две эквивалентные операции, связывающие две точки и вектор. Первая - это вычитание точек, которая формирует из двух точек Р и Q вектор v (рис. 4.5). Эту операцию запишем следующим образом:

v = P-Q.

'Поскольку в этой книге в основном используется язык С, а не С+ -i- и поскольку OpenGL не является объектно-ориентированным пакетом, нам приходится пользоваться в примерах несколько устаревшими конструкциями вроде typedef или struct.

4.1. Скаляры, точки и векторы

Следствием такого определения операции вычитания точек является то, что для заданной точки и вектора v существует единственная точка Р, которая удовлетворяет приведенному выше соотношению. Это утверждение можно формально выразить следующим образом: пусть заданы точка () и вектор г, тогда существует точка Р, такая, что Таким образом, Р формируется с помощью операции сложения вектора с точкой. Правило сочленения начала вектора с концом другого вектора позволяет очень наглядно представить операцию сложения векторов (рис. 4.6,а). Из правила сложения векторов следует и отношение, справедливое для любых трех точек Р,() и Я (рис. 4.6,6):

(Р-О) + (О-Я) = Р-Я.

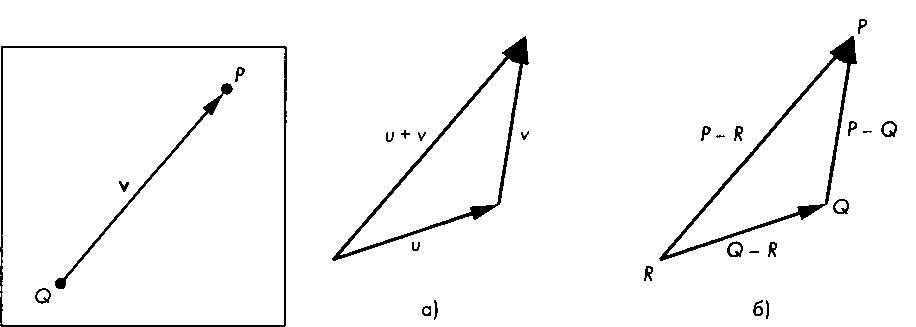
Рис. 4.5. Вычитание точек Рис. 4.6. Правило сочленения начала одного вектора с концом другого"opengl5_170.html">⇐ Предыдущая| |Следующая ⇒