Теперь, используя наши познания в аффинных преобразованиях, выведем уравнение матрицы проецирования, формируемой в OpenGL. Нам предстоит для этого решить две задачи. Сначала с помощью преобразования сдвига передвинем центр заданного параллелепипеда в центр канонической зоны видимости - начало координат. Затем изменим масштабные коэффициенты таким образом, чтобы каждое ребро параллелепипеда имело длину 2 единицы (рис. 5.33). Следовательно, имеем два преобразования:
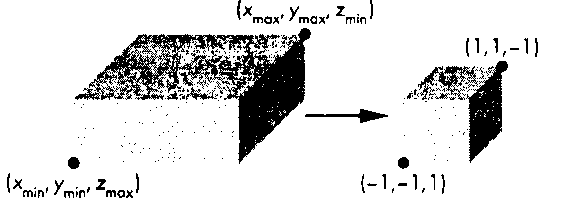
Рис. 5.32. Соответствие между заданным параллелепипедом видимости и канонической зоной видимости
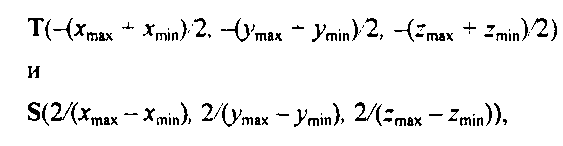
Визуализация
после суперпозиции которых сформируется матрица проецирования"images/tmpB6CA-208.png" alt="Аффинные преобразования в процессе нормализации">
Рис. 5.33. Аффинные преобразования в процессе нормализации Поскольку ось проецирования камеры направлена вдоль отрицательной полуоси г, проецирующие лучи направлены из бесконечности отрицательного полупространства в начало координат. В терминах расстояния до передней и задней отсекающих плоскостей - параметрах 1пеаг и Наг вызова функции дЮг1"images/tmpB6CA-209.png">
5.7.3. Косоугольная проекция Использование функции glOrtho( ) позволяет создавать в OpenGL ограниченный класс параллельных проекций - только такие, в которых проецирующие лучи ортогональны картинной плоскости. Но во многих приложениях желательно иметь и косоугольные проекции5. Можно, конечно же, самостоятельно сформировать соответствующую матрицу поэлементно, но попробуем воспользоваться той же идеей, которую разработчики OpenGL применили при формировании матрицы ортогонального проецирования, - найдем преобразование желаемой проекции в каноническую проекцию предварительно искаженных объектов.
Косоугольная проекция характеризуется углом между проецирующими лучами и картинной плоскостью (рис. 5.34). В графической системе, которая поддерживает параллельное проецирование в общем виде, зона видимости для косоуголь-
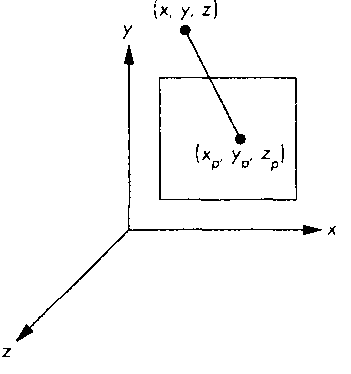
ные 5.34. Косоугольная проекция точки
'Обращаю ваше внимание на то. что без косоугоіьного проецирования не удалось бы вычерчивать оси координат в рисунках этой книги (см упр. 5.15).
