При работе с криволинейными поверхностями способ вычисления компонентов вектора нормали существенно зависит от принятого способа описания такой поверхности. В главе 10 будут проанализированы три разных метода представления кривых и криволинейных поверхностей. Здесь же мы покажем несколько способов определения нормали к сферической поверхности единичного радиуса, центр которой совпадает с началом координат. Обычно такая сфера описывается уравнением в неявной форме (implicit equation):
j\x,y,z) = x2+y2 + z2-\=0,или в векторной форме: Лр) = р-р-1 =0.
Нормаль определяется вектором градиента (gradient vector), который обычно представляется в виде матрицы-столбца:
"Э/
~2х
= 2р
дх
ÈLду
к
2у 2z
Сфера может быть описана и уравнением в параметрической форме (parametric form). При этом координаты x,ywz любой точки на сферической поверхности представляют собой независимые уравнения от двух параметров, и и v: х = х(и, v), у=у\и, v), z = z(u, v).
Как будет показано в главе 10, в системах компьютерной графики предпочтение следует отдать параметрической форме, особенно при описании кривых и поверхностей, хотя некоторые виды поверхностей имеют несколько вариантов параметрического представления. К ним принадлежит и сфера. Один из вариантов параметрической системы уравнений сферы имеет вид х(и, v) = cosu sinv, у(и, v) = COSM cosv, z(u, v) - sin;/.
Изменяя и и v в диапазоне -тс/2 < и < тс/2, -тс/2 < v < я/2, получим все точки на сфере. Используя параметрическое представление поверхности, нормаль можно вычислить как характеристику касательной плоскости (tangent plane) в точке р(м, v) = [х(и, v) у(и, v) z(u, v)]r (рис. 6.20). Получить уравнение касательной плоскости можно на базе линейных членов разложения параметрических функций х(и, v), у(и, v), z(u, v) в ряд Тейлора в окрестности точки р. Прямые, параллельные векторам и и проходящие через точку р, лежат в ка ои ov
сательной плоскости. Векторы и - определяются следующим образом: о и dv
Закрашивание
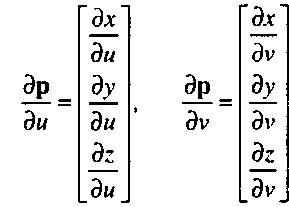
Вектор нормали формируется как векторное произведение:
