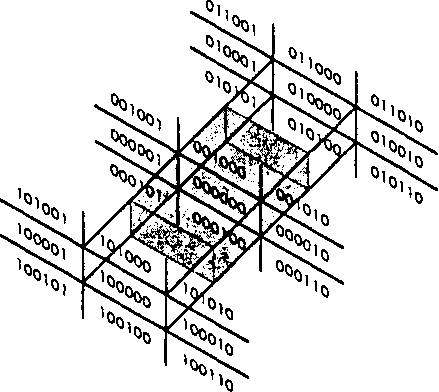
Рис. 7.22. Разбиение пространства на области при использовании трехмерной модификации алгоритма Коэна-Сазерленда
7.6. Отсечение в трехмерном пространстве Но главные изменения по сравнению с двухмерным случаем заключаются в том, что для вычисления точек пересечения сопоставляются прямая и плоскость, а не прямая и прямая. При вычислении точек пересечения используется параметрическое представление прямой и плоскости (рис. 7.23). Обозначив через п вектор нормали к плоскости, а через р0- точку, лежащую в этой плоскости, запишем систему уравнений, решением которой является значение параметра а для точки пересечения прямой с плоскостью"images/tmpB6CA-309.png">
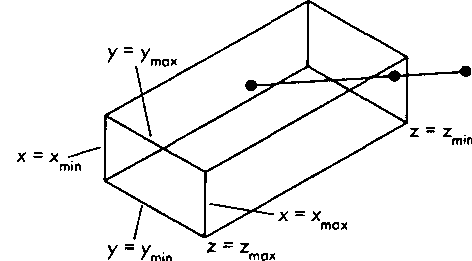
Рис 7.23. Пересечение прямой с плоскостью
Рис 7.24. Отсечение при ортогональном проецировании Несколько сложнее обстоит дело при использовании косоугольного проецирования (рис. 7.25). В этом случае зона видимости уже не является правильным параллелепипедом, а ее грани не параллельны координатным плоскостям. Вот тут-то нам и поможет нормализация проецирования, которую мы рассматривали в главе 5. Эта процедура позволяет привести косоугольную проекцию к ортогональной, выполнив предыскажение исходного объекта. Преобразование скоса превращает косоугольный параллелепипед зоны видимости в правильный. На рис. 7.26,а представлен вид сверху на косоугольный параллелепипед видимости, внутри которого находится отображаемый объект - куб, до выполнения преобразования. Эти же объекты после выполнения нормализации показаны на рис. 7.26,6. Если с точки зрения проективного преобразования количество вычислений, необходимых для косоугольного проецирования или нормализации и ортогонального проецирования, одно и то же, то отсечение в последнем случае выполняется гораздо проще. Именно поэтому следует отдать предпочтение использованию нормализации проецирования. Приведенный пример показывает, насколько важно ана-
