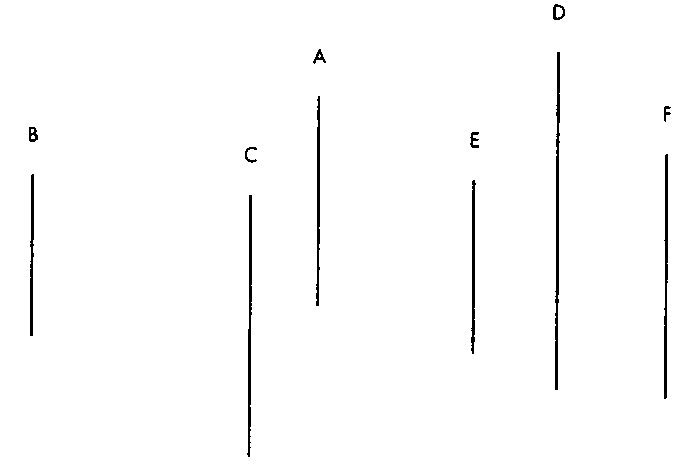
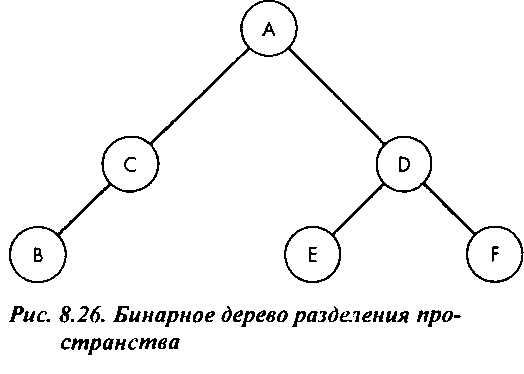
Рис. 8.25. Вид сверху на разделяемые многоугольники Плоскость многоугольника А разделяет все многоугольники на две группы, одна из которых содержит В и С (они находятся перед плоскостью А), а вторая - многоугольники D, Е и F. которые находятся за плоскостью А. С этой плоскости мы начнем формирование бинарного дерева разделения пространства (BSP - binary spatial-partition tree). Узлы этого дерева представляют плоскости, разделяющие пространство (плоскости многоугольников, входящих в состав сцены), а ребра задают последовательность разделения. В корне бинарного дерева на рис. 8.26 находится многоугольник А, многоугольники В и С принадлежат левому поддереву, a D, Е и F - правому. Просматривая дерево рекурсивно, приходим к выводу, что С расположен за плоскостью многоугольника В, а в правом поддереве плоскость D разделяет многоугольники Е и F. Обращаю ваше внимание на то, что одна и та же конфигурация многоугольников может быть по-разному представлена с помощью бинарного дерева пространственного разбиения. Форма дерева существенно зависит от порядка разбиения, т.е. порядка, в котором обрабатываются многоугольники в ходе формирования дерева. В общем случае, если обнаруживается, что плоскость некоторого многоугольника разрезает другие многоугольники, пересекаемый многоугольник разделяется на два, первый из которых помещается в левое поддерево, а второй - в правое, подобно тому, как мы поступали в главе 7 при реализации алгоритма сортировки.
8.9. Другие типы древовидных структур
Это дерево может использоваться при выводе на экран образов многоугольников, причем для обхода дерева используется алгоритм обратного обхода в центрированном порядке (bachvard in-order traversal). В соответствии с этим алгоритмом дерево обходится рекурсивно. В каждом цикле сначала "посещается" правое поддерево, потом корень, а затем левое поддерево.
Одно из главных достоинств бинарных деревьев разделения пространства состоит в том, что одно и то же дерево можно использовать при формировании изображения, видимого разными наблюдателями (с разных точек зрения). Наблюдатель может переместиться, например, в противоположный угол сцены, как показано на рис. 8.27, а мы сможем сформировать порядок вывода образов многоугольников, обходя дерево с помощью стандартного центрированного порядка обхода, - левое поддерево, корень, правое поддерево (когда наблюдатель располагался так, как на рис. 8.24, мы использовали обратный центрированный порядок). Обращаю ваше внимание также на то, что алгоритм выполняется рекурсивно во всех тех случаях, когда можно разделить множество многоугольников или любых объектов на группы, называемые кластерами (clusters). Следовательно, сгруппировав многоугольники в многогранник, можно затем сгруппировать многогранники в кластеры и рекурсивно применять алгоритм к кластерам. В приложениях типа симуляторов полета, для которых модель остается практически неизменной в процессе работы программы, а меняется в основном только положение наблюдателя, использование бинарных деревьев рассмотренного типа позволяет с высокой скоростью формировать изображение, которое "видит" пилот из кабины летящего самолета. Дерево содержит всю информацию об объектах сцены и их расположении относительно друг друга, а положение наблюдателя определяет выбор алгоритма обхода дерева.
