Описать кубическую полиномиальную кривую можно следующим образом, воспользовавшись матрицами-строками и матрицами-столбцами: л

р(и) = с0 +с,м + с,н2 +с3м3 = ]£сАм* =urc,

*=0

где

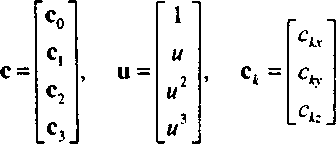
Кривые и криволинейные поверхности

В этих выражениях с представляет матрицу коэффициентов полинома. Именно ее нам и потребуется вычислить по заданному ансамблю опорных точек. Ниже мы рассмотрим разные классы кубических кривых, которые отличаются характером сопоставления с опорными точками. Для каждого типа будет сформирована система из 12 уравнений с 12-ю неизвестными, но, поскольку параметрические функции для компонентов х,у и г независимы, эти 12 уравнений будут разделены на три группы по 4 уравнения с 4-мя неизвестными.

Вычисление значений коэффициентов определенного типа кубической кривой выполняется по заданному ансамблю опорных точек, соответствующих некоторым значениям независимого параметра и. Эти данные могут иметь форму ограничений, требующих, чтобы формируемая полиномиальная кривая проходила через некоторые из заданных точек и в окрестности других точек. Кроме того, эти данные накладывают и определенные условия на гладкость кривой, например, первая производная и производные более высоких порядков должны быть непрерывными в заданных точках сопряжения отдельных сегментов. Та или иная формулировка этих условий определяет класс формируемой кривой, причем кривые разного класса, сформированные на одном и том же ансамбле опорных точек, могут существенно отличаться.

10.4. Интерполяция Первым мы рассмотрим класс кубических интерполяционных полиномов (interpolating polynomial). Хотя этот класс кривых очень редко используется в задачах компьютерной графики, их анализ поможет вам составить четкое представление о характеристиках полиномиальных кривых общего вида и о тех операциях, которые необходимо выполнять при формировании кривых других классов.

Пусть имеется четыре опорные точки в трехмерном пространстве: р0, Pi, Рг и р3. Каждая точка представлена тройкой своих координат:

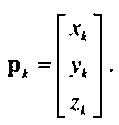
Наша задача- отыскать элементы матрицы коэффициентов с, такие, что полином р(м)=и7с будет проходить через заданные четыре опорные точки. Вывод соответствующих соотношений особого труда не представляет. Мы располагаем четырьмя трехмерными точками, через которые должна проходить формируемая кривая. Следовательно, можно составить 12 уравнений с 12 неизвестными- элементами матрицы с. Но сначала нужно решить, какому значению независимого параметра и соответствует каждая опорная точка. Не располагая никакой другой информацией, кроме координат точек и порядка их размещения вдоль формируемой кривой, будем считать, что значения ик (к=0,..,3) распределены равномерно на интервале [0, 1], т.е. и=0, 1/3, 2/3, 1 (напоминаю, мы договорились, что параметр и изменяется только на интервале [0, 1]). Соответствующие четыре уравнения в векторной форме имеют вид

⇐ Предыдущая| |Следующая ⇒