Рис. 10.15. Влияние длины векторов касательных на форму сегмента полиномиальной кривой

10.6. Кривые и поверхности в форме Безье Сравнение кривых в форме Эрмита и в форме интерполяционного полинома чем-то напоминает сравнение яблока и апельсина. Обе формы представляют кубические полиномиальные кривые, но для их формирования используют разные по характеру наборы данных. Следовательно, нельзя сравнить кривые в этих формах, сформированные на одном и том же наборе данных. Попробуем использовать один и тот же ансамбль опорных точек и для определения интерполяционного полинома, и для косвенного задания производных в форме Эрмита. В результате получим кривую в форме Безье (Bezier), которая является очень хорошим приближением кривой в форме Эрмита и которую можно сравнивать с интерполяционным полиномом, сформированным на том же ансамбле опорных точек. Кроме того, поскольку определение кривой в форме Безье не требует задания производных, такая процедура идеально подходит для интерактивного построения криволинейных объектов в системах компьютерной графики и автоматизации проектирования.

10.6.1. Кривые Безье Рассмотрим ансамбль из четырех опорных точек р0, рь р2 и р3. Зададимся условием, что конечные точки формируемой кривой р(м) должны совпадать с опорными точками р0 и р3: Ро = Р(0), Рз = Р(1).

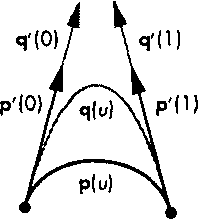
Безье предложил использовать две другие опорные точки р, и р2 не для интерполяции, а для задания производных в крайних точках сегмента и=0 и и=1. Мы воспользуемся для этого линейной аппроксимацией в пространстве параметра (рис. 10.16):

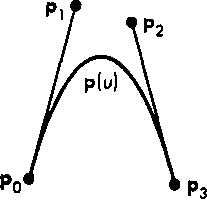
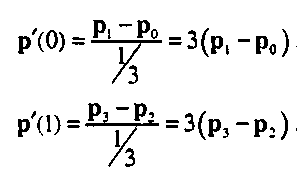
Рис. 10.16. Аппроксимация векторов касательных

Применив эту аппроксимацию к касательным в двух крайних точках к параметрической полиномиальной кривой р(!/)=иус, получим два условия"opengl5_482.html">⇐ Предыдущая| |Следующая ⇒