444 Глава 10. Кривые и криволинейные поверхности

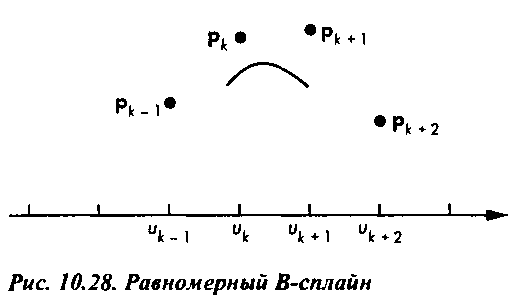
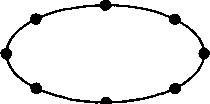
Рис. 10.29. Периодический равномерный В-сплайн

10.8.3. Неравномерные В-сплайны

При повторении узлов (кратности узлов) проявляется эффект приближения сформированного В-сплайна к опорной точке, ассоциированной с этими узлами. Если кратность узла равна d+1, то В-сплайн степени d будет проходить через соответствующую опорную точку. Следовательно, один из методов решения проблемы недостатка данных для формирования сплайна состоит в том, чтобы повысить кратность узлов, соответствующих начальной и конечной точкам, и тем самым "заставить" результирующую кривую пройти через эти точки. При этом остальные, внутренние, узлы остаются равноотстоящими. Такие В-сплайны называются открытыми (open splines).

Для формирования кубических В-сплайнов часто используется массив узлов {0,0,0,0, 1,2,…, п, п, п, п}. Особый интерес представляет массив узлов {0,0,0,0, 1,1,1,1}, который превращает В-сплайн в кривую Безье. В общем случае можно делать кратными и внутренние узлы, а также размещать их неравномерно.

10.8.4. NURBS - неравномерный рациональный В-сплайн Анализируя В-сплайны, мы полагали, что р(и) представляет собой массив триад [ х(и) у(и) z(u)]T. При работе в двухмерном пространстве триада заменяется парой [х(и) у(и)]', но все выведенные соотношения остаются неизменными. Точно так же соотношения не изменятся и в том случае, если мы перейдем к четырехмерным В-сплайнам. Трехмерные опорные точки р,=[*/ у, z,] можно следующим образом представить в пространстве однородных координат"opengl5_492.html">⇐ Предыдущая| |Следующая ⇒