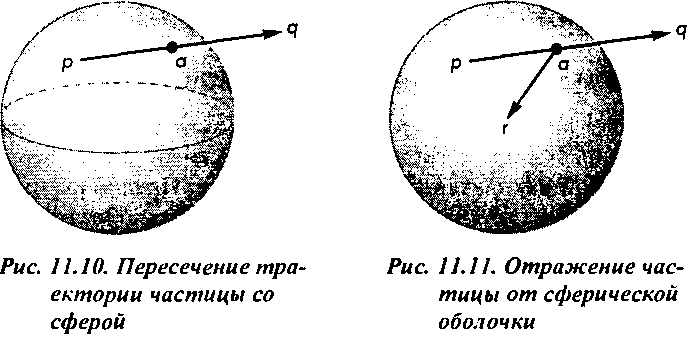
Следовательно, в момент времени 1+И частица будет в точке а+аг. Для дальнейших вычислений потребуется также определить и новый вектор скорости \ч частицы после отражения от сферической оболочки. Компонента вектора скорости вдоль направления нормали в точке столкновения равна п\р. Нам нужно изменить направление этой компоненты на противоположное, оставив другие компоненты без изменений. Текст программы, реализующей
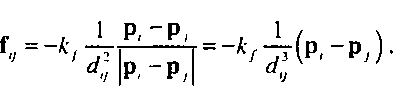
Глава Л. Процедурные методы
описанную модель системы частиц, заключенных в сферическую оболочку, вы найдете в файле bounce.с. В упражнениях в конце главы вам будет предложено самостоятельно разработать другие варианты подобного рода ограничений.
11.5.3. Мягкие ограничения Включение в физическую модель большинства видов жестких ограничений связано с серьезным увеличением сложности, а значит, и времени вычислений. Если, например, требуется, чтобы скорость всех частиц не превосходила некоторую максимальную или чтобы сумма энергии всех частиц не превышала некоторую константу, то для решения такой задачи в реальном масштабе времени потребуется очень мощный процессор, поскольку обычных дифференциальных уравнений для описания состояния системы будет недостаточно.
Но во многих ситуациях можно получить удовлетворительное решение, используя мягкие ограничения в виде минимизации некоторого функционала качества системы. Если, например, желательно, чтобы частица, занимающая в текущем состоянии положение р, не удалялась слишком далеко от точки р0, то можно включить в модель функгрпо штрафа {penalty function) |р-ро|2. Чем меньшее значение этой функции будет обеспечено в текущем состоянии, тем точнее соблюдает система сформулированное таким образом ограничение. Эта функция является одним из видов энергетической функции (energy function) системы, величина который является оценкой энергии определенного вида, накопленной в системе. Физически это может быть потенциальная или кинетическая энергия. При использовании энергетической функции в качестве меры состояния системы в модели может решаться задача минимизации или максимизации этой оценки, но описание соответствующих математических методов выходит за рамки данной книги.
