U =A*„ уР -к), где
х, = х0+/'Лх, У/ = Уо+^У, z, = z0+kAz.
Каждое значение fljk можно считать результатом усреднения скалярного поля в правильном параллелепипеде со сторонами Ах, Ау, Дг, центр которого находится в точке (x„ypzk). Такой
12.3. Визуализация поверхностей и скалярных полей
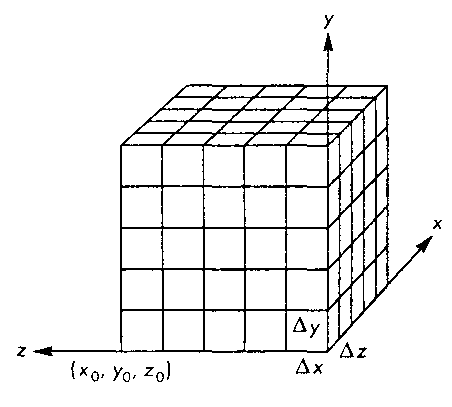
А/с. /2./6. Объемное множество данных
элементарный параллелепипед будем называть векселем (voxel) по аналогии с пикселем - элементарной областью двухмерной плоскости.
Трехмерный массив значений скалярного поля, соответствующих вокселям, называется структурированным множеством данных (structured data set), поскольку при его хранении нет
смысла хранить еще и информацию о размещении каждой выборки в пространстве. Термины структурированное множество данных и множество векселей (set of voxels) зачастую используют как синонимы.
Данные, снятые в произвольных точках пространства, должны храниться совместно с координатами соответствующих точек, а потому их принято называть неструктурированным множеством данных. Визуализация неструктурированного множества данных выполняется несколько сложнее, но, в конце концов, все сводится к тем же самым методам. Поэтому эту проблему мы специально исследовать не будем.
Способов наглядного представления скалярного поля можно придумать даже больше, чем способов отображения функции двух переменных. Однако из всего множества наибольшую популярность завоевали два - непосредственное отображение объема и построение изоповерхностей. При непосредственном отображении объема в формировании изображения "принимает участие" каждый воксель, а при построении изоповерхностей в конкретном изображении используется только подмножество вокселей. Для функции fx, у, г) изоповерхность определяется уравнением в неявной форме:
fx, у, г) = с.
Значение константы с - уровень изоповерхности. Наша задача - отыскать приемлемый способ аппроксимации изоповерхности по заданному множеству вокселей.
12.3.2. Визуализация функций, заданных в неявной форме Задача визуализации изоповерхностей функции трех переменных является естественным расширением задачи построения линий уровня функции двух переменных. Рассмотрим функцию трех переменных, заданную в неявной форме:
