у = (1-0с + «х,ге[0,1]. (1.73) Тогда из условия принадлежности проекции плоскости (1.70) получаем
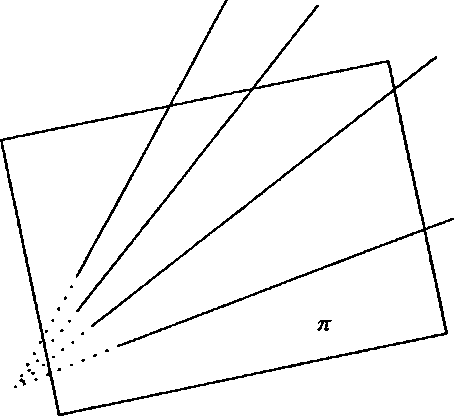
Рис. 1.9
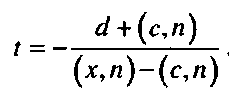
(1.74)Координаты и их преобразования
Как видно из этой формулы, перспективное преобразование не является аффинным преобразованием (на самом деле это преобразование принадлежит к классу дробно-линейных преобразований). Тем не менее это преобразование также можно записать при помощи матрицы однородного преобразования.
Выпишем каноническое уравнение перспективного проектирования. Пусть центр проектирования равен (О, О, -I)7 , а картинная плоскость задается уравнением г = 1
Тогда проекцией произвольной точки (<хл,хг,хъ) будет точка
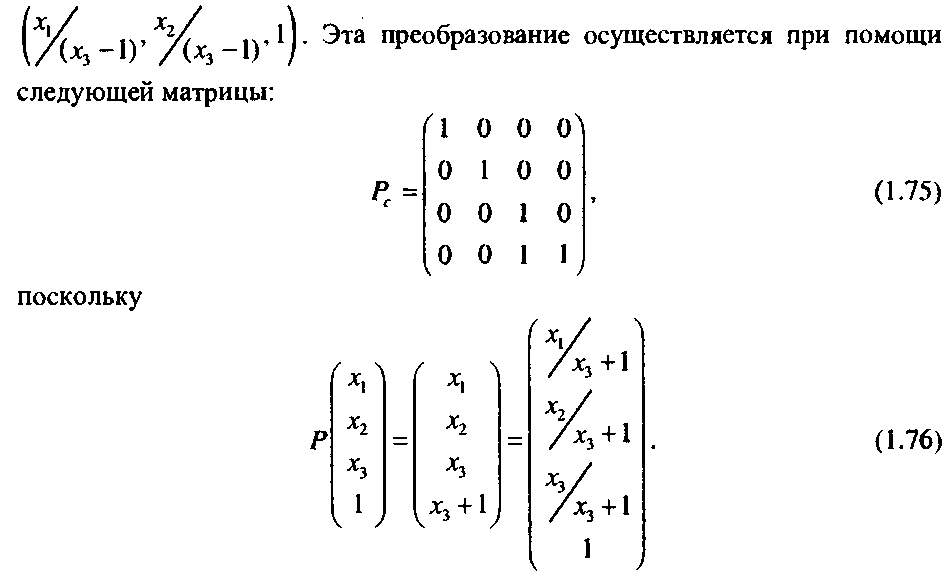
Таким образом, как произвольное аффинное преобразование, так и параллельное и перспективное проектирование может быть записано при помощи матриц однородных преобразований.
Более подробно о координатах и преобразованиях можно прочитать в[1],[13].
УДАЛЕНИЕ НЕВИДИМЫХ ПОВЕРХНОСТЕЙ
Одной из очень важных задач при рендеринге сложных трехмерных сцен является определение того, какие части объектов (ребра, грани), находящихся в трехмерном пространстве, будут видны при заданном способе проектирования, а какие будут закрыты от наблюдателя другими объектами. В качестве возможных видов проектирования традиционно рассматриваются параллельное и центральное (перспективное). Плоскость, на которую осуществляется проектирование, будем далее называть картинной (рис. 2.1).
Несмотря на кажущуюся простоту, задача удаления невидимых линий и поверхностей является достаточно сложной и зачастую требует очень больших объемов вычислений. Поэтому существует целый ряд различных методов решения этой задачи, включая и методы, опирающиеся на аппаратные решения.
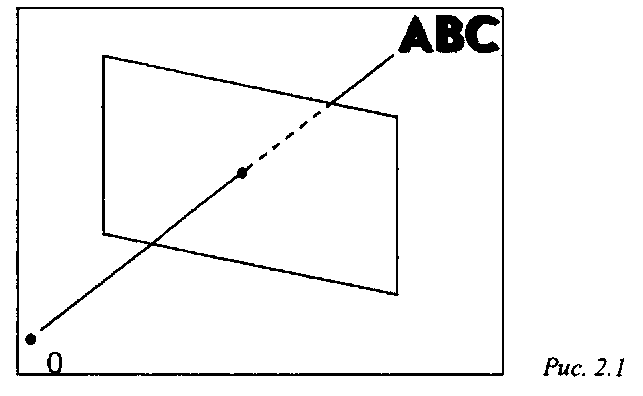
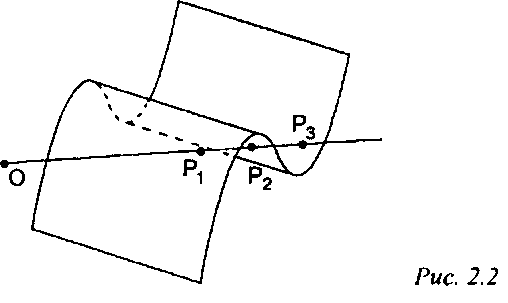
Удаление невидимых поверхностей
Эти методы различаются по следующим основным параметрам (рис. 2.3)"images/tmpFE1D-40.png" alt="3">
Рис. 2.3
