Метод classify служит для классификации ААВВ относительно плоскости.
Для проверки точки на принадлежность служит метод contains.
Метод isEmpty служит для проверки того, является ли заданное ААВВ пустым.
Метод intersects служит для проверки двух ААВВ на пересечение.
Метод reset служит для "обнуления" заданного ААВВ и обычно применяется перед построением ААВВ по набору точек.
Метод getVertex позволяет получить координаты вершины ААВВ по ее индексу (от 0 до 7).
Метод getCenter возвращает координаты центра данного ААВВ.
Метод merge служит для объединения двух ААВВ.
Методы grow, move и apply служат для применения заданных преобразований к ААВВ.
Можно в качестве ограничивающих тел использовать прямоугольные параллелепипеды произвольной ориентации (Oriented Bounding Box-OBB): В = {с + осе, + Ре2 + уе}, \а\ < 1, |р| < 1, |у| < l}, (3.9)
где с - центр параллелепипеда; е1, е2, еъ - ортогональные векторы, определяющие его оси.
Если задан набор точек у0, у,, уп_,, то в качестве центра ОВВ можно выбрать их среднее
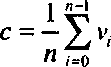
(3.10)а векторы е{,е2,еъ определяются как промасштабированные собственные векторы матрицы
М=^1>,-с)(у,-с)7. (3.11)
Несмотря на то что проверка попадания точки внутрь ОВВ довольно проста, хотя и сложнее, чем для ранее рассмотренных тел, проверка на пересечение двух ОВВ является достаточно сложной из-за того, что они могут иметь разные наборы осей. Один из алгоритмов для осуществления такой проверки основан на теореме о разделяющей оси - ищется такая прямая, чтобы проекции двух ОВВ на нее не пересекались бы. Проверяются следующие 15 осей: по 3 направляющие оси для каждого ОВВ и 9 осей, являющихся результатом векторного произведения этих осей между собой (рис. 3.11).
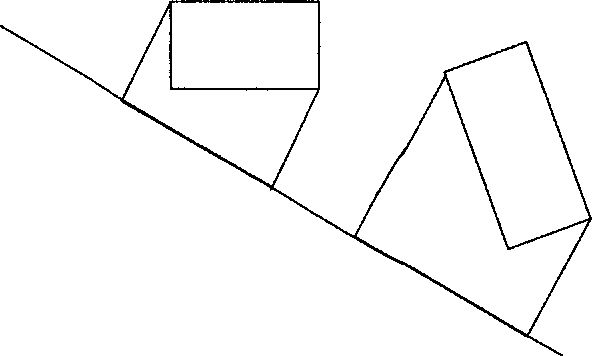
Рис. 3.11
Проверка на содержание одного ОВВ внутри другого также достаточно трудоемка.
Объединение двух ОВВ может быть сделано достаточно просто - в качестве направляющих осей объединения достаточно взять направляющие оси одного из ОВВ.
