МасштабированиегЛ »........: . -л-.у^ щи *«-иьшфЦ)Л
Масштабирование вдоль координатных осей задается при помощи матрицы !
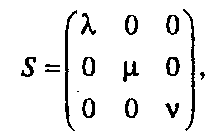
(І.19)где коэффициенты Л., Ц, V > 0.
Отражение Отражение относительно плоскости Оху задается матрицей

Отражение относительно остальных координатных плоскостей задается аналогично.
Перенос
Преобразование переноса на вектор а в пространстве R3 задается формулой у = х + а. (1.21)
По аналогии с классами Vector2D, Matrix2D и Transform2D удобно ввести соответствующие классы для работы в трехмерном пространстве. Их полный исходный код находится на компакт-диске.
Однородные координаты
Удобно представить все аффинные преобразования в матричном виде. С этой целью вводятся так называемые однородные координаты.
Каждому вектору х = (хр х2, х3)г е R3 можно поставить в соответствие вектор х = (хр х2, x3,lf е R* При этом в пространстве R* векторов вида
(дг,, х2, х3, wf можно произвести факторизацию, поставив в соответствие произвольному вектору (дгр х2, х3, wf, w Ф 0 вектор (х, fw,x2f w, х3 I w, if. Тогда любой прямой, проходящей через начали координат и состоящей из точек вида (w*p wx2, wx3, wf, будет поставлен в соответствие вектор
(хр х2, х3,1)7. Тем самым множество векторов /?4\{0} факторизуется на классы эквивалентности, где каждый такой класс представлен вектором вида (хр х2, х3,1)г.
Такие четырехмерные векторыс вводимым описанным выше отношением эквивалентности называются однородными координатами.
Координаты и их преобразования
Рассмотрим преобразования в пространстве однородных координат.
Определение. Матрица Н = [ку), 1 </, ]<4 называется матрицей однородного преобразования, если ки = 1.
Произвольное однородное преобразование Н можно записать в сле дующем виде:
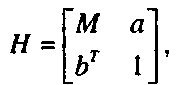
(1.22)где М - матрица 3x3, а а и Ъ - трехмерные векторы.
Произвольному линейному преобразованию (1.3) в трехмерном пространстве соответствует следующее однородное преобразование:
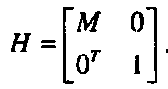
(1.23)Сдвиг на вектор а можно также представить при помощи однородного преобразования
