ПРОВЕРКИ “ВНУТРИ-СНАРУЖИ”
В различных графических процессах часто приходится определять внутренние области объектов. Распознавание внутренней области такого простого объекта, как выпуклый многоугольник, окружность или сфера, - процесс, как правило, не сложный. Однако иногда приходится иметь дело с более сложными объектами. Например, может понадобиться описать такую сложную закрашенную фигуру с пересекающимися сторонами, как на рис. 3.46. В подобных ситуациях не всегда понятно, какие участки плоскости ху следует называть “внутренними”, а какие - “внешними”. Существует два общепринятых алгоритма определения внутренних областей плоских фигур - это правило четного-нечетного и правило ненулевого числа витков.
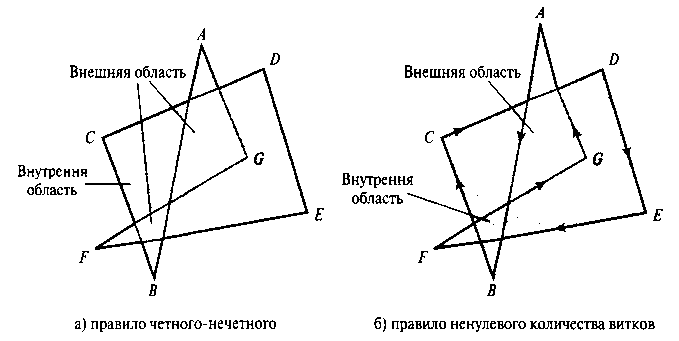
Рис. 3.46. Определение внутренних и внешних участков замкнутой ломаной линии, содержащей самопересекающиеся элементы
Чтобы воспользоваться правилом четного-нечетного, которое еще называют правилом проверки на четность, сначала мысленно проведем прямую линию, соединяющую любую точку Р с какой-то удаленной точкой за пределами области координат замкнутой ломаной линии. Затем сосчитаем количество точек пересечения этой прямой с прямолинейными отрезками. Если число отрезков, пересекающих линию, четное, тогда точка Р считается внутренней. В противном случае точка Р - внешняя. Чтобы найти точное количество точек пересечения с отрезками, нужно убедиться в том, что выбранная прямая не проходит через концы отрезков. На рис. 3.46, а показаны внутренние и внешние области, полученные в результате применения правила четного-нечетного для самопересекающейся замкнутой ломаной линии. Этой процедурой можно воспользоваться, например, для заполнения заданным цветом внутренней области между двумя концентрическими окружностями или многоугольниками.
Еще один способ определения внутренних областей - это правило ненулевого количества витков, при котором считается, сколько раз граница объекта “оборачивается” (“наматывается”) вокруг отдельной точки в направлении против часовой стрелки. Это число называют количеством витков, а внутренние точки двухмерного объекта можно определить по тому, имеют ли они ненулевое количество витков. Правило ненулевого количества витков применяется таким образом: сначала количество витков устанавливаем равным 0, а затем опять представляем себе прямую линию, соединяющую точку Р с удаленной точкой за пределами области координат объекта. Выбранная прямая не должна проходить ни через один конец отрезка. При перемещении по этой линии от точки Р до удаленной точки считается количество прямолинейных отрезков, принадлежащих объекту, которые пересекают эту опорную линию в каждом направлении. При каждом пересечении прямой с отрезком в направлении справа налево к количеству витков прибавляется 1, а при пересечении с отрезком, идущим слева направо, отнимается 1. Конечное значение числа витков, поеле учета всех пересечений с границами определяет относительное положение точки Р. Если число витков не равно нулю, то точка Р считается внутренней точкой. В противном случае Р относится к внешним точкам. На рис. 3.46, б показаны внутренние и внешние области, определенные с помощью правила ненулевого числа витков для самопересекающейся, замкнутой ломаной линии. Для таких простых объектов, как многоугольники и окружности, правило ненулевого числа витков и правило четного-нечетного дают одинаковые результаты. Но для более сложных форм эти два метода могут дать различные внутренние и внешние области, как показано на рис. 3.46.
