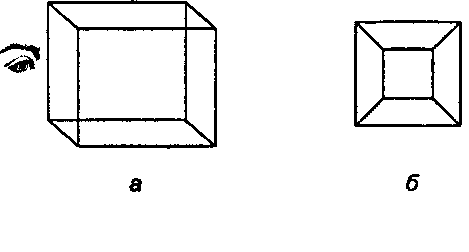
Рис. 6.12. Диаграммы Шлегеля для куба Еще несколько примеров приведено на рис. 6.13. Рисунок 6.13, а - это диаграмма Шлегеля для объекта ПИРАМИДА с рис. 6.8, б, а на рис. 6.13, б\\ 6.13, в показаны две различные диаграммы для базового сарая. (Какие грани являются ближайшими для наблюдателя?)
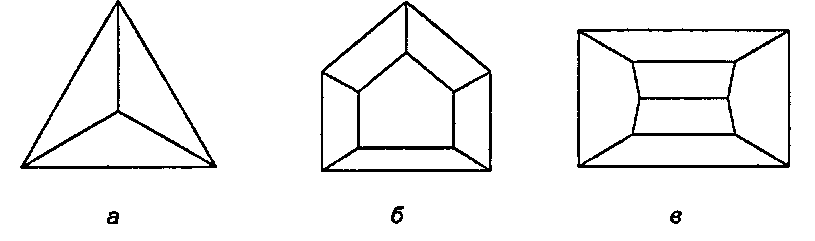
Рис. 6.13. Диаграммы Шлегеля для ПИРАМИДЫ и базового сарая
6.3. Многогранники
6.3.1. Призмы и антипризмы
Призма - это частный случай полиэдра. Она обладает некоторой симметрией и поэтому довольно проста в описании. Как показано на рис. 6.14, призма получается в результате заметания (sweeping), или выдавливания (extruding - экструзия), полигона вдоль прямой линии, что превращает двумерный полигон в трехмерный полиэдр. На рис. 6.14, а полигон Р перемещается вдоль вектора d, в результате чего формируется полиэдр, приведенный на рис. 6.14, в. Если вектор d перпендикулярен к плоскости Р, то призма называется прямой призмой (right prism). На рис. 6.14, в показано несколько печатных букв алфавита, превращенных в призмы.
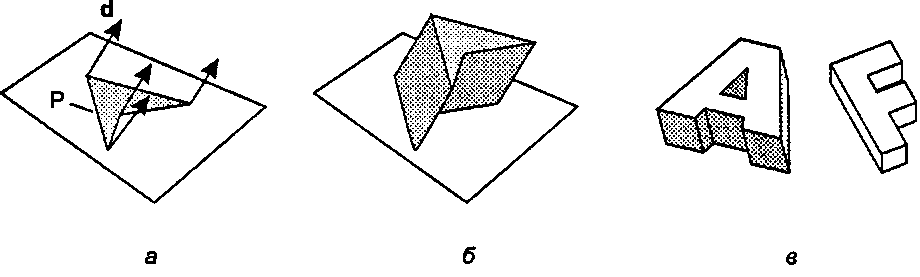
Рис. 6.14. Формирование призмы
Будем называть правильной (regular) такую призму, которая имеет в основании правильный полигон, а в качестве боковых граней - квадраты1. На рис. 6.15, а показана шестиугольная правильная призма. Некоторым отклонением от правильной призмы является антипризма (antiprism), показанная на рис. 6.15, б. Она не является «выдавленным» объектом"images/tmp8E4A-371.png" alt="Правильная призма и антипризма">
Рис. 6.15. Правильная призма и антипризма Практические упражнения 6.3.1. Составление списка для призмы
Составьте списки вершин, нормалей и граней для призмы, приведенной на рис. 6.16. Пусть основание этой призмы (грань № 4) лежит в плоскости ху, а вершина 2 - на оси г при 2 = 4. Предположим далее, что вершина 5 располагается в трех единицах вдоль оси х и что основание призмы - равносторонний треугольник.
