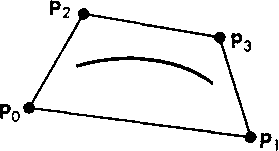
10.7.2. В-сплайны и базисные функции Рис. 10.23. Выпуклая оболочка сегмента сплайновой кривой Попробуем взглянуть на формируемую кривую с несколько иной точки зрения - какое влияние оказывает на форму кривой каждая отдельная опорная точка. Каждая опорная точка принимается во внимание при формировании четырех последовательных сегментов составной В-сплайновой кривой. Это свойство гарантирует локальный характер кривых этого класса, т.е. изменение положения отдельной точки влияет на поведение составной кривой в достаточно малой окрестности этой точки. Рассмотрим опорную точку р,. На интервале между и=0 и и=\ координаты этой точки являются весовыми коэффициентами для полиномиальной функции смешивания Ь2(и). Они также учитываются и при формировании сегмента ц(и) слева, где эти координаты являются весовыми коэффициентами функции смешивания Ьх(и+1), - для этого сегмента нам придется сдвинуть значение параметра и на 1.
Общий взнос отдельной опорной точки можно выразить в виде В,(и)р„ где В,(и) имеет вид График этой функции показан на рис. 10.24. Задавшись множеством опорных точек р0,…,рт, можно выразить составной сплайн в виде единого выражения": р(М)=2>»р,.
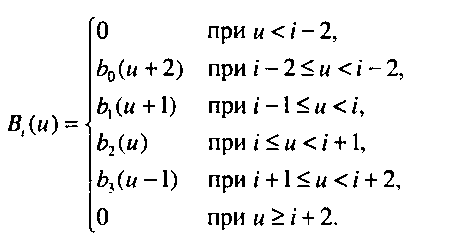
Из этого выражения следует, что каждый член множества функций В(и-1) является сдвинутым образом единственной функции и что такое множество образует базис для всех кубиче10Если вы посчитаете условия класса С2 слишком жесткими, то можно обеспечить выполнение условий только класса О? и получить дополнительную степень свободы при конструировании кривых такого типа. Подробнее этот вопрос рассматривается в работе Барского (ВагБку) [Ваг83].
11 Условия для начального и конечного сегментов составного сплайна мы рассмотрим в разделе 10.8.
10.7. Кубические В-сплайны
ских В-сплайновых кривых. Задавшись ансамблем опорных точек, мы формируем кусочно-полиномиальную кривую р(и) на всем интервале представления параметра в виде линейной комбинации отдельных базисных функций. На рис. 10.25 показаны кривая р(и) и базисные функции, которые входят в состав взвешенной суммы. В теории сплайнов общего вида, которую мы кратко рассмотрим в разделе 10.8, эта идея распространяется на полиномы более высокой степени и вариант аппроксимации, когда разные сегменты составной сплайн-кривой представлены полиномами разной степени.
