Поэкспериментировать с простой IFS можно с помощью карманного калькулятора. Введите любое (положительное) число пит и нажмите кнопку «квадратный корень». Результатом будет новое число, \/пит. Нажмите кнопку «квадратный корень» еще раз, чтобы вычислить квадратный корень из нового числа, а именно yjy/num. Повторяйте это, пока не надоест. Посредством данной операции вы итерируете функцию квадратный корень, причем каждый результат используется как входные данные для следующего квадратного корня. При начальном значении пит = 64 генерируется последовательность: 64, 8, 2,8284, 1,68179.....(Существует ли величина, к которой эта последовательность сходится?)

На рис. 2.27 приведена схема этой системы итерируемых функций, показывающая, что каждое значение на выходе вводится обратно для получения квадратного корня, снова и снова.

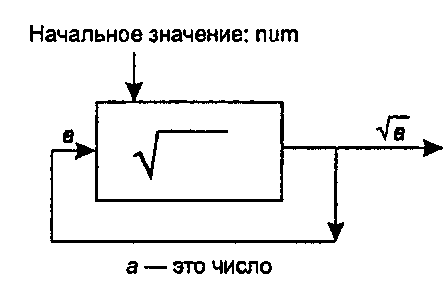
Рис. 2.27. Повторное вычисление квадратного корня В данном примере итерируемой функцией является f(x) - Vjc или символически /(.) = так называемый «извлекатель квадратного корня» («square rooter»). В качестве функции/(.) могут выступать и другие функции, например такие"opengl1_129.html">⇐ Предыдущая| |Следующая ⇒