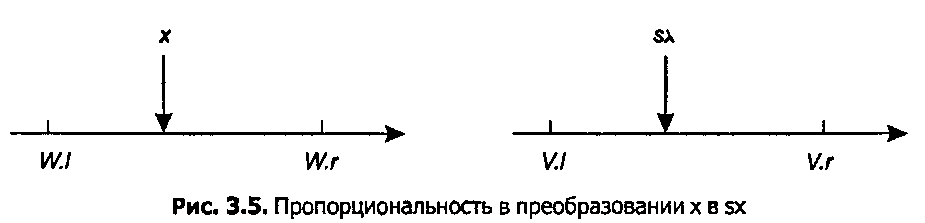
3.2. Мировые окна и порты просмотра Как определить А, В, Си £>? Сначала рассмотрим преобразование для х. Как видно из рис. 3.5, пропорциональность требует, чтобы разность (хг-У./) составляла ту же долю от разности (Кг-УД которая составляет величина (х-№.Г) от величины (\V.r-WJ), следовательно: бх-УІ _ х-УУ.1 Ух-VI ~ УУх-\У1
или Ух - VI („, Ух-У.1 „Л
ях = -х + У.1--\У1 .
\Vx-WI У \Vx-WI }
Обозначив множитель при х буквой А, а свободный член - буквой С, получим:
_ Ух-У.1 УУх-1¥.1
и С = V1 - А\¥1.
Подобным же образом пропорциональность для у означает, что Бу-УЬ _ у-УУ.Ъ Уі-УЬ ~ 1¥1-1¥Ъ'
а запись ву в виде Ву + О требует соотношений У1-УЬ
В = , Б = УЪ-В\¥Ь.
УУ1-\У.Ъ
В результате мы имеем следующие формулы преобразования мирового окна в порт просмотра: £с - Ах + С
и їу=Ву + Д
где А =Ух-У1 с = у1_АШ (3-3) \Vx-WI
в = ул ¥ъ, о = у.ь-в^ь.
ИЛ/-ИЛА
Это преобразование можно использовать для любой точки (х, у) внутри или вне окна. Точки внутри окна преобразуются во внутренние точки порта просмотра, а точки вне окна - в точки вне порта просмотра. Следует тщательно сверить следующие свойства этого преобразования, используя равенства (3.3):
1. Если х находится на левом краю окна (х = то яг находится на левом краю порта просмотра (я* - V.!);
2. Если х - на правом краю окна, то - на правом краю порта просмотра.
3. Если х составляет/-ю часть от ширины окна, то яд: является/-й частью от ширины порта просмотра.
4. Если х находится вне окна слева от него (х < 1У./), то яд: также находится вне порта просмотра слева (хг < V./), и аналогично в случае, когда х вне окна справа от него.
Проверьте аналогичные свойства для преобразования г/ в яг/.
Дополнительные инструменты для рисования
Пример 3.2.1
Рассмотрим окно и порт просмотра, изображенные на рис. 3.6. Окно имеет размеры (и7./, У/.г, У/.Ь, ¥/.г) = (0,2,0, 0,1,0), а порт просмотра - (К/, У.г, У.Ь, У.г) - (40, 400, 60, 300).
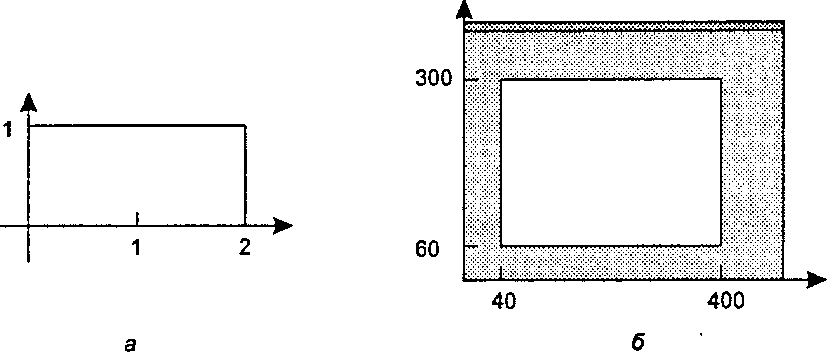
Рис. 3.6. Пример окна (а) и порта просмотра (б)
