3.7. Рисование окружностей и дуг

Рис. 3.41. Логотип университета штата Массачусетс 3.6.14. Вращающиеся пентаграммы: анимация На рис. 3.42 изображена пентаграмма, повернутая на некоторый угол относительно Пентагона, причем соответствующие их вершины соединены. Напишите программу, анимирующую эту фигуру. Данная композиция нарисована с использованием некоторого начального угла А поворота пентаграммы. После короткой паузы эта пентаграмма стирается, а затем снова рисуется с немного большим углом А. Процесс повторяется до нажатия любой клавиши.

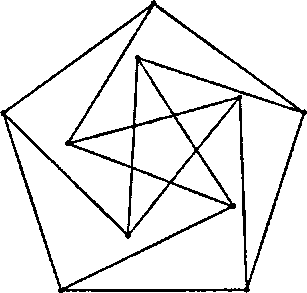
Рис. 3.42. Вращающиеся пентафигуры

3.7. Рисование окружностей и дуг Рисование окружности эквивалентно рисованию я-угольника с большим числом вершин. Этотя-уголь-ник напоминает окружность (если его не изучать слишком пристально). Подпрограмма drawCircleO, представленная в листинге 3.13, рисует правильный 50-угольник методом простой передачи своих параметров в ngonO. Было бы более целесообразно написать drawCircleO с нуля, основываясь на коде листинга 3.11.

Листинг 3.13. Рисование круга на базе 50-угольника

линк. куботейнеры от производителя.

void drawCircle(Point2 center, float radius) {
const int numVerts = 50"images/tmp8E4A-125.png" alt="Задание дуги">
Рис. 3.43. Задание дуги Нам нужна подпрограмма drawArcO, рисующая дугу окружности. Функция, приведенная в листинге 3.14, аппроксимирует дугу как часть и-угольника с использованием команд moveToO и lineToO. Последовательные точки дуги находятся вычислением cos( ) и sin( ) каждый раз внутри главного цикла. Если величина sweep отрицательна, то угол автоматически убывает.





⇐ Предыдущая| |Следующая ⇒