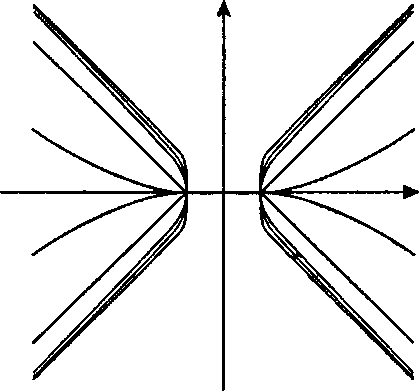
Рис 3.60. Семейство супергипербол
3.8.4. Формы в полярных координатах
Для представления ряда интересных кривых можно использовать полярные координаты. Как показано на рис. 3.61, каждая точка кривой задана углом 0 и радиальным расстоянием г. Если и г и 9 являются функциями от t, то при изменении t развертывается кривая (г(с), 0(0)- Конечно, эту кривую можно представить и в декартовых координатах (x(t), y(t)), где
*(f) = r(Ocos(0(O), , 1Q
y(t) = r(Osin(0(O). V'™>3.8. Применение параметрического задания кривой
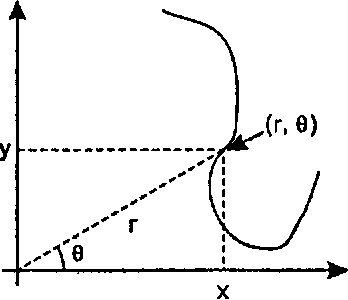
Рис 3.61. Полярные координаты
Однако для большинства замечательных кривых возможно упрощение. В этих случаях радиус г выражается явной функцией от 0, причем параметром, пробегающим всю кривую, является сам угол 0. Для каждой точки (г, 0) соответствующая точка в декартовых координатах (х, у) вычисляется по формулам"images/tmp8E4A-150.png" alt="Примеры кривых, задающихся простыми формулами в полярных координатах Конические сечения (эллипс, парабола и гипербола) имеют общую полярную форму записи">
Рис. 3.62. Примеры кривых, задающихся простыми формулами в полярных координатах Конические сечения (эллипс, парабола и гипербола) имеют общую полярную форму записи:
