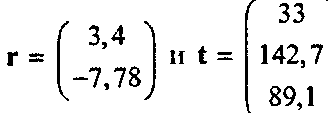
Это имеет значение, когда нам нужно умножить точку или вектор на матрицу, как мы увидим в главе 5.
1 Для точек обычно используются большие буквы, а для векторов - маленькие жирные.
4.2. Обзор векторов
4.2.1. Операции с векторами С векторами можно проделывать две основные операции: их можно складывать и умножать на скаляры (scalars) (вещественные числа)'. Итак, если а и b - два вектора, as - скаляр, то будут иметь смысл следующие выражения: а + b и sa. Если, например, а = (2,5, 6), a b = (-2, 7,1), то мы можем построить следующие два вектора: а + Ь = (0,12, 7)
и
m65 куртка. Передний бампер на Лада гранту цена. Цена передний бампер для Лада гранта.
6а = (12, 30, 36), причем все эти операции всегда выполняются покомпонентно (componentwise).
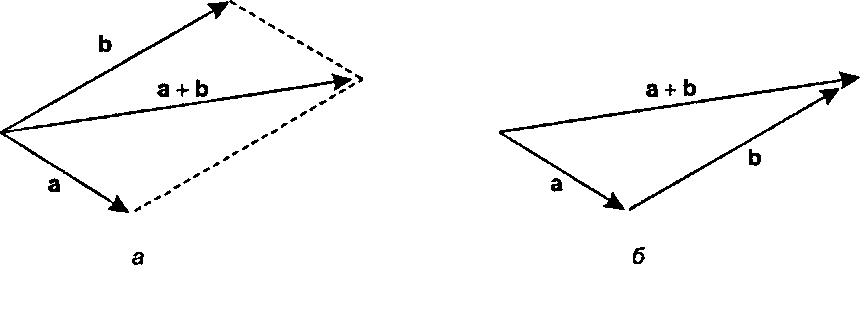
Рис. 4.5. Сумма двух векторов На рис. 4.5 показан пример сложения двумерных векторов а = (1, -1) и Ь = (2,1). Графически сложение двух векторов можно представить двумя способами. На рис. 4.5, а оба вектора показаны «исходящими» из одной и той же точки и образующими таким образом две стороны параллелограмма. Тогда сумма этих векторов равна диагонали параллелограмма - той диагонали, которая исходит из общего начала этих векторов. Этот рисунок - так называемое «правило параллелограмма» для сложения векторов - является обычной картиной сложения сил, действующих в точке; тогда диагональ будет результирующей силой.
С другой стороны, на рис. 4.5, б показан случай, когда один вектор (Ь) начинается из конца другого (а), а их сумма изображена соединяющей начало вектора а с концом вектора Ь. Суммарный вектор замыкает треугольник, который представляет собой обыкновенное сложение одного перемещения с другим. Ясно, что компоненты суммы равны сумме компонентов ее слагаемых, как и предписывает алгебра.
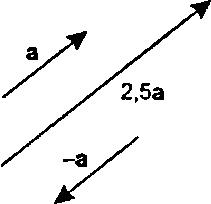
Рис. 4.6. Масштабирование векторов На рис. 4.6 показан эффект масштабирования векторов. Для х = 2,5 вектор ха имеет то же направление, что и а, но в 2,5 раза длиннее. При отрицательном х направление ха противоположно направлению а. На рисунке приведен случай х = -1.
Вычитание легко выводится из понятий сложения и масштабирования"opengl1_221.html">⇐ Предыдущая| |Следующая ⇒