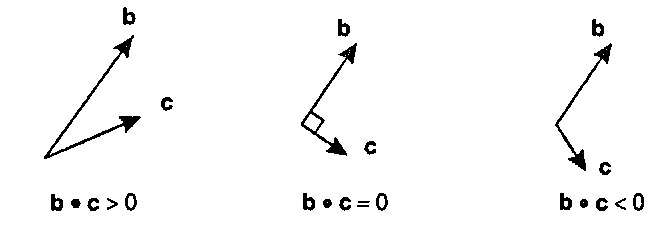4.3.3. Знак Ь с и перпендикулярность
Напомним, что соэ(9) положителен, если |б| меньше 90°, равен нулю при |8| = 90° и отрицателен, если |9| превышает 90°. В силу того, что скалярное произведение двух векторов пропорционально косинусу угла между ними, мы можем сразу определить, что угол между двумя векторами (любой длины, отличной от нуля) составляет: менее 90°, если Ь с > 0; ровно 90°, если Ь с = 0; (4.16) более 90°, если Ь с < 0.
Все эти результаты приведены на рис. 4.10. Знак скалярного произведения используется во многих алгоритмических тестах.
Рис. 4.10. Знак скалярного произведения Особенно важным является случай, когда векторы расположены под углом 90°, то есть перпендикулярны. Определение. Векторы b и с называются перпендикулярными, если ь-с = 0. (4.17)
Иногда вместо слова «перпендикулярны» употребляют синонимы: ортогональны (orthogonal) и нормальны (normal), и мы будем пользоваться всеми этими тремя словами попеременно. Вектор, перпендикулярный прямой или плоскости, также иногда будем называть нормалью.
Наиболее известными примерами ортогональных векторов являются те, которые расположены вдоль осей дву- и трехмерных систем координат, как показано на рис. 4.11. На рис. 4.11, а двумерные векторы (1,0) и (0,1) являются взаимно перпендикулярными единичными векторами. Трехмерные аналоги этих векторов употребляются столь часто, что их называют «стандартными единичными векторами» (координатными ортами) и обозначают буквами i, j, k.
Определение. Координатными ортами в трехмерном случае называются векторы, имеющие следующие компоненты: і = (1,0,0), j - (0,1, 0), к - (0,0,1). (4.18)
На рис. 4.11, б показаны эти три орта в правосторонней системе координат, а на рис. 4.11, в - в левосторонней системе. Отметим, что к всегда указывает на положительное направление оси z.
С помощью приведенных определений можно записать любой трехмерный вектор (а, Ь, с) в альтернативной форме:
(а, Ь, с) = йі + b'i + ск. (4.19)