Это равносильно известному факту, что перпендикулярные прямые имеют взаимно обратные и различающиеся знаком угловые коэффициенты (к, - -1/к2). В главе 5 мы увидим, что операция «переставить и сменить знак» (interchange and negate*) естественным образом появляется в связи с поворотом на 90°.
4.3. Скалярное произведение мальным к вектору а. Существует бесчисленное множество векторов, нормальных к любому вектору а, так как любое скалярное кратное (scalar multiple) вектору b, то есть вектор Ь, умноженный на скаляр, например (-21,12) и (7, -4), тоже нормально к а. (Нарисуйте на бумаге несколько таких векторов для заданного а.)
Удобно иметь символ для одного исключительного вектора, нормального к заданному двумерному вектору а. Для этой цели мы будем использовать символ «1» («регр», произносится «перп»). Определение. Пусть а = (ах, ау). Тогда
^ = '-ау1ах) (4.20) называется перпендикулярным против часовой стрелки (counterclockwise perpendicular) к а.
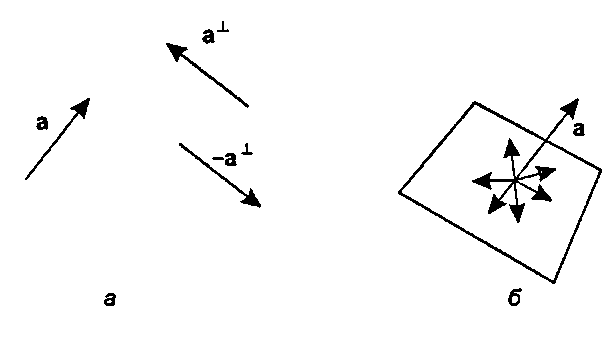
Рис. 4.12. Вектор а1, перпендикулярный к а Отметим, что а и а1 имеют одну и ту же длину"opengl1_230.html">⇐ Предыдущая| |Следующая ⇒
