Ввиду того, что векторное произведение сводится к вычитанию различных величин (см. равенство 4.28), данный метод нахождения вектора п является чувствительным к погрешностям вычислений, особенно когда угол между а и Ь мал. Позднее мы рассмотрим более устойчивый метод для практического нахождения нормальных векторов.

Практические упражнения

4.4.8. Значение выбора точек Получится ли та же самая плоскость, как в примере 4.4.3, если мы возьмем те же точки в другом порядке, например: а = (1,0,2) - (2,3,0) и Ь = (1,2,4) - (2,3,0)? Докажите, что в результате получится та же самая плоскость.

4.4.9. Нахождение плоскостей Для каждой тройки точек найдите нормальный вектор (если он существует) к плоскости, проходящей через эту тройку: О Р1 = (1,1,1), Р2 = (1,2,1), Р3 = (3,0,4).

О Р1~ (8,9,7), Р2 = (-8, -9, -7), Р3 = (1,2,1).

О Р, = (6,3, -4), Р2 = (0,0,0), Р3 = (2,1, -1).

О Р, = (0,0,0), Р2 = (1,1,1), Р3 = (2,2,2).

4.4.10. Нахождение нормальных векторов Вычислите нормальные векторы к каждой грани двух объектов, изображенных на рис. 4.17. Куб имеет вершины в точках (±1, ±1, ±1), а вершины тетраэдра расположены в точках (0,0,0), (0,0,1), (1,0,0) и (0,1,0).

4.5. Отображение ключевых геометрических объектов В предыдущих разделах мы обсуждали некоторые основные положения теории векторов и их приложения к важным геометрическим проблемам, возникающим в графике. Теперь мы рассмотрим ряд фундаментальных идей, облегчающих работу с прямыми и плоскостями, являющимися центральными объектами в графике, поскольку их «прямизна» и «плоскостность» обеспечивает простоту их отображения и работу с ними.

4.5. Отображение ключевых геометрических объектов

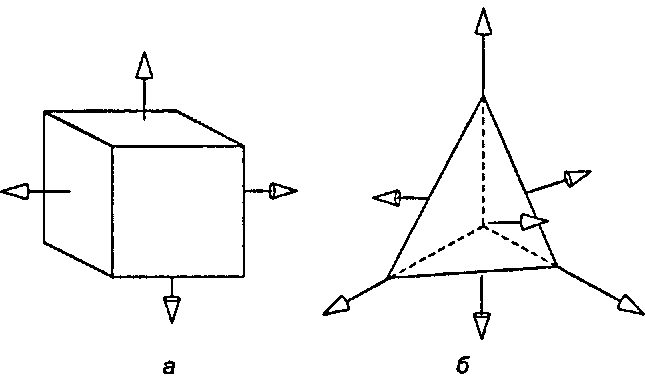
Рис. 4.17. Нахождение нормальных векторов к граням Что означает «представить» прямую или плоскость и почему это важно? Задача состоит в том, чтобы получить формулу или уравнение, с помощью которого можно определять, какие точки лежат на прямой, а какие - нет. Это могло бы быть уравнение, которому удовлетворяют все точки данной прямой, и только они. Или это могла бы быть функция, возвращающая различные точки прямой при изменении некоторого параметра этой функции. Такое представление позволяет ответить на следующие вопросы"opengl1_238.html">⇐ Предыдущая| |Следующая ⇒