Практические упражнения
4.5.3. Предельный случай твининга Какой будет эффект твининга в случае, когда все точки А. ломаной А одни и те же? Как искажается вид ломаной В в каждом твине?
4.5.4. Экстраполяция Пусть ломаная Л является квадратом с вершинами (1,1), (-1,1), (-1, -1) и (1, -1), а ломаная В - клином с вершинами (5, -2), (4,3), (4,0) и (3, -2). Нарисуйте (от руки) форму Р(г) для t = -1, -0,5, 0,5 и 1,5.
4.5.5. Экстраполяция и твининг Пусть рядом изображены пять рисунков из ломаных линий. Произведя тщательные вычисления, вы обнаружили, что три средних рисунка являются промежуточными между первым и последним, а также вычислили использованные при этом значения г. Но кто-то утверждает, что на самом деле последний рисунок является экстраполяцией первого и четвертого. Существует ли какой-нибудь способ выяснить, так ли это на самом деле? Если это экстраполяция, то можно ли вычислить, какое значение t использовалось при этом? Если можно, то чему оно равно?
Векторные инструменты для графики
4.5.5. Обзор: квадратичный и кубический твининг и кривые Безье В главе 11 мы будем заниматься вопросами проектирования сложных форм, называемых кривыми Безье (Bezier curves). Основная идея заключается в обычном твининге между множеством точек. В случае линейной интерполяции мы «разбиваем единицу» на части (1 - г) и t и используем эти части в качестве «весовых коэффициентов» для точек А и В. Мы можем распространить этот прием на квадратичную интерполяцию, разбивая единицу на три части. Написав следующее выражение:
1-((1-г) + 02, мы обобщаем нашу формулу на случай трех частей (1 -t)2,2(1 - t)t и t2. Очевидно, что их сумма равна единице, поэтому эти части можно использовать для формирования аффинной комбинации точек А, В и С:
P(t) - (1 - t)2A + 2t( l-t)B + t2C. (4.38)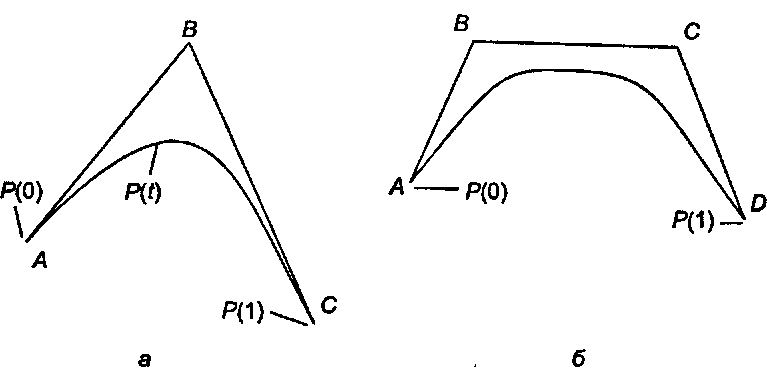
Рис. 4.24. Кривые Безье как твининг Это и есть кривая Безье для точек А, В и С. На рис. 4.24, а показана форма P(t) при изменении t от 0 до 1. Данная кривая плавно переходит от Л к С. (Обратите внимание, что кривая пропускает среднюю точку.) Продвигаясь дальше, можно разбить 1 - ((1 - г) +t)3 на четыре части (какие?), которые могут быть использованы для «кубической интерполяции» между точками А, В, Си D, как показано на рис. 4.24,6.
