L(t) = C+bt. (4.39)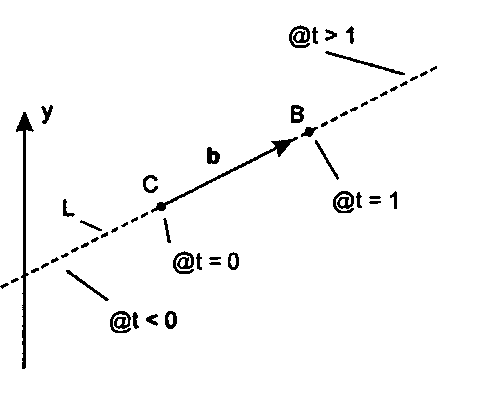
I-^ х
Рис. 4.26. Параметрическое представление прямой L(t)
По мере изменения t положение точки L(t) перемещается вдоль прямой. Часто под параметром t подразумевают время и используют для описания различных частей прямой такую терминологию: «в момент времени 0», «с течением времени» или «позднее». На рис. 4.26 показаны вектор Ь и прямая L, проходящие через точки Си В (проиллюстрирован двумерный случай, однако в трехмерном используются те же понятия). Отметим, где располагается положение точки L(t) для различных значений t. При t - 0 положение L(t) соответствует точке С, поэтому мы говорим, что при t = 0 мы находимся «в точке» С. При t = I L(l) = С + (В - С) = В. По мере изменения t мы добавляем к точке С большее или меньшее значение вектора Ь, получая в результате новую точку вдоль прямой. Если t больше 1, то новая точка располагается где-нибудь за точкой В относительно С; если же t меньше 0, то новая точка располагается на прямой за точкой С относительно В.
Для фиксированного значения t, например t «= 0,6, равенство (4.39) дает формулу для ровно одной точки прямой, проходящей от С к В, а именно точки 1(0,6). Таким образом, данное равенство описывает точку. Но в силу того, что это равенство можно рассматривать как функцию от t, генерирующую координаты каждой точки на прямой L по мере изменения t, это равенство называется параметрическим представлением прямой L.
Векторные инструменты для графики
Прямая, луч и отрезок на рис. 4.25 могут быть представлены с помощью той же функции 1(г) из равенства (4.39). Эти объекты отличаются друг от друга только промежутком изменения входящего в равенство параметра t.
для отрезка прямой 0 < t < 1; для луча 0 < г < о°; (4.40)
ДЛЯ ПрЯМОЙ ЛИНИИ -оо < t < о°.
Луч «начинается» в точке С при t - 0, проходит через точку В при г = 1 и затем продолжается до бесконечности по мере роста г. Точку С обычно называют «начальной точкой» такого луча.
