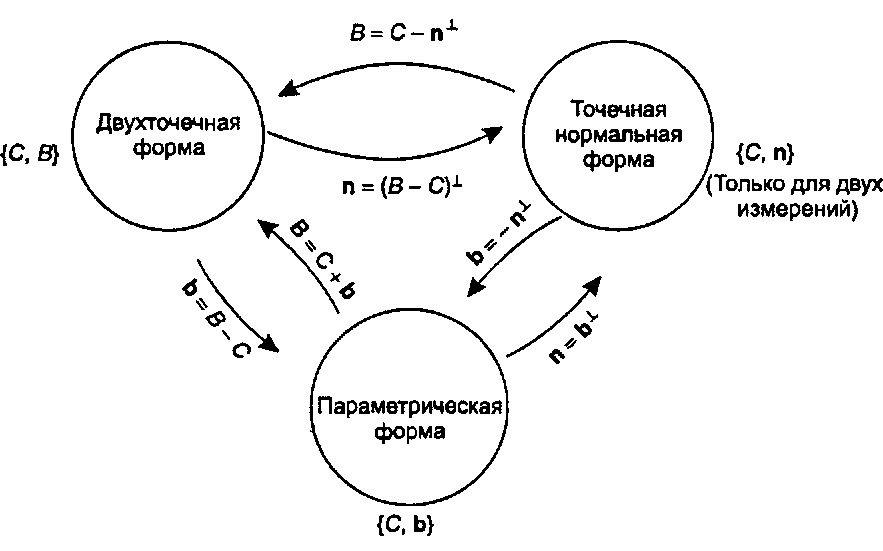
Рис. 4.28. Переход между представлениями прямой Практическое упражнение

4.5.7. Нахождение точечной нормальной формы

Найдите точечную нормальную форму для прямой, проходящей через точки (-3,4) и (6, -1). Нарисуйте на миллиметровке эту прямую и нормальный к ней вектор.

Плоскости в трехмерном пространстве Поскольку в трехмерной графике интенсивно используются многоугольники, кажется, что плоскости появляются всюду. Многоугольник («грань» объекта) располагается в плоскости своего «родителя», и нам часто приходится отсекать объекты относительно плоскостей или находить плоскость, в которой располагается определенная грань.

Подобно прямым, плоскость имеет три основные формы"images/tmp8E4A-208.png" alt="Параметрическое задание плоскости">

Рис. 4.29. Параметрическое задание плоскости Заметим, что в параметрическое выражение поверхности включены два параметра, в то время как для кривой требуется только один параметр. И действительно, если один из параметров зафиксирован (скажем, s = 3), то Р(3, t) уже является функцией одной переменной и представляет прямую линию"opengl1_255.html">⇐ Предыдущая| |Следующая ⇒