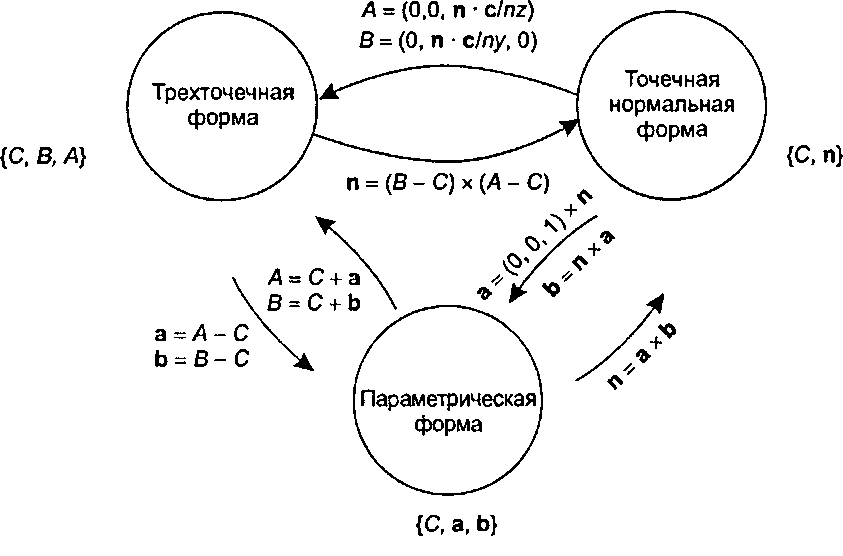
Рис. 4.31. Переход между представлениями плоскости

Векторные инструменты для графики

В параметрической форме уравнения (4.43) значения s и t могут изменяться от -°° до °°, поэтому плоскость может простираться неограниченно. В ряде случаев мы хотим иметь дело только с «куском» плоскости, например, с расположенным в этой плоскости параллелограммом. Такой кусок носит название плоского лоскута (planar patch), этот термин позволяет вообразить плоскость в виде лоскутного одеяла (quilt), сшитого из множества соединенных вместе кусочков. Позднее мы будем изучать криволинейные поверхности, сшитые из лоскутов, которые не обязательно будут плоскими. Большая часть практического моделирования объемных тел сводится к собиранию в одно целое лоскутов различной формы для создания поверхности объекта.

ros-znak.com цвета сигнальные знаки безопасности.

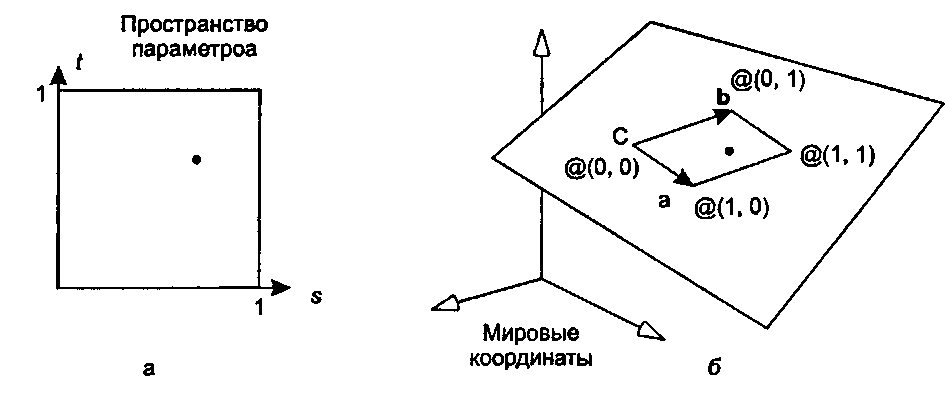
Рис. 4.32. Преобразование из одного пространства в другое для определения плоского лоскута Плоский лоскут формируется посредством ограничения диапазона допустимых значений параметров s и t. Например, часто требуют, чтобы s и t изменялись только от 0 до 1. Лоскут позиционируется и ориентируется в пространстве с помощью соответствующего подбора векторов а, b и точки С. На рис. 4.32, а показана область допустимых значений s и t в виде квадрата в пространстве параметров (parameter space), а на рис. 4.32, б показан лоскут, который получается при таком ограничении в пространстве объекта (object space).

Каждой точке (s, t) в пространстве параметров соответствует одна трехмерная точка на лоскуте P(s, t) = С + as + Ы. Такой лоскут является параллелограммом, углы которого соответствуют четырем углам в пространстве параметров и расположены следующим образом"opengl1_259.html">⇐ Предыдущая| |Следующая ⇒