Треугольник на рис. 4.40, б имеет три ограничивающих прямые. (Какое уравнение имеет каждая из этих прямых?) Точечные нормальные формы этих трех прямых имеют следующий вид:

(-1,0)(Р-(0,0)) = 0; (0,-1)(Р-(0,0))-0; (1,1)(Р-(1,0)) = 0.

Отметим, что в каждом случае используется внешняя нормаль.

Большое преимущество работы с выпуклыми полигонами состоит в том, что проверка на пересечение выполняется только относительно бесконечных прямых, и нет необходимости проверять, расположена ли точка пересечения «по другую сторону» от концевой точки. (Вспомните сложность тестов на пересечение в предыдущем разделе.) Кроме того, в случае выпуклых полигонов можно использовать точечную нормальную форму, что упрощает вычисления.

эгопласт тендер обязательная аудиторская проверка аудит 2008.

Для выпуклого полиэдра в трехмерном пространстве каждая плоскость имеет внутреннее и внешнее полупространство и внешний нормальный вектор. Полиэдр является пересечением всех внутренних

Векторные инструменты для графики

полупространств (множеством всех точек, одновременно находящихся во внутренних полупространствах каждой ограничивающей плоскости).

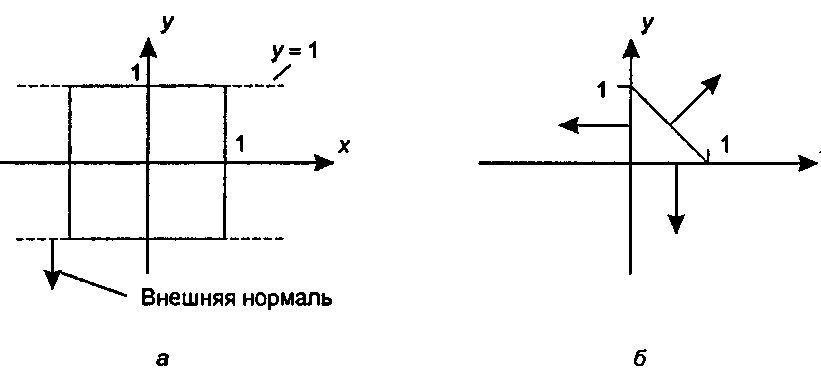
Рис. 4.40. Примеры выпуклых полигонов

4.8.2. Пересечение с лучами и отсечение для выпуклых полигонов В разделе «Пересечения прямых с плоскостями; отсечение» мы разработали метод нахождения точки соударения луча с отдельной прямой линией или плоскостью. Мы можем использовать этот метод для нахождения точки соударения луча с выпуклым полигоном или полиэдром.

Задача пересечения На рис. 4.41 показан луч А + с?, пересекающийся с выпуклым полигоном Р. Мы хотим узнать все точки пересечения этого луча с Р. Поскольку полигон Р - выпуклый, то луч пересекает его ровно два раза"opengl1_270.html">⇐ Предыдущая| |Следующая ⇒