4.8.3. Нахождение отсеченной прямой Определите, какая часть отрезка прямой с концевыми точками (2,4) и (20,8) расположена внутри четырехугольного окна с углами (0,7), (9,9), (14,4) и (2,2).

4.8.4. Отсечение границами произвольных полигонов В предыдущем разделе мы видели, как осуществляется отсечение отрезка прямой границами выпуклого полигона. Расширим эту процедуру до метода отсечения отрезка границами любого полигона.

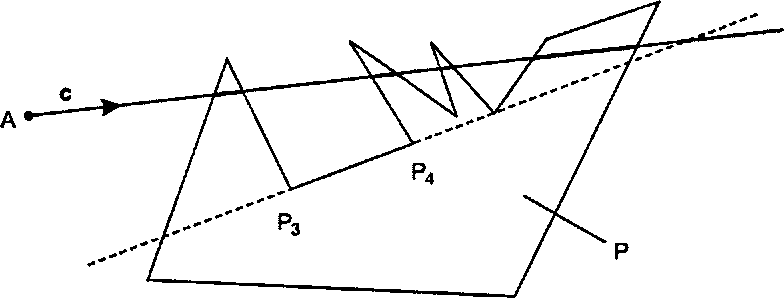
Рис. 4.45. Когда луч находится внутри произвольного полигона Р?

Основная задача состоит в том, чтобы найти, когда луч A+ct расположен внутри полигона Р, заданного списком вершин Р0, Р,,…, PN_V Пример приведен на рис. 4.45.

Ясно, что в общем случае луч может входить в полигон Р и выходить из него много раз и что результат отсечения отрезка границами Р может привести не к одному отрезку, а к целому списку отрезков. Кроме того, полигон Р более не описывается набором бесконечных ограничивающих прямых в точечной нормальной форме; мы вынуждены работать с ЛГ-конечными отрезками типа Р3Р4, из которых формируются его ребра.

Данная задача близка к той, с которой мы уже имели дело в разделе «Пересечения прямых с плоскостями; отсечение»"opengl1_277.html">⇐ Предыдущая| |Следующая ⇒