О середины отрезков, соединяющих ортоцентр треугольника (точка пересечения трех высот) с его вершинами.

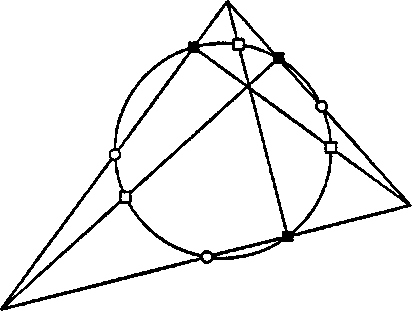
Рис 4.49. Девятиточечная окружность

Примечательно, что через все девять точек проходит единственная окружность! На рис. 4.49 показана девятиточечная окружность1 для произвольного треугольника. Такую девятиточечную окружность, наверно, проще всего нарисовать как окружность, проходящую через середины сторон треугольника.

Тематическое задание 4.3. Находится ли точка <2 внутри выпуклого полигона Р?

Уровень сложности II.

Задан выпуклый многоугольник Р. Пусть требуется определить, находится заданная точка 0, внутри полигона Р или нет. Однако во время изучения выпуклых полигонов в разделе «Работа с выпуклыми полигонами и полиэдрами» мы выяснили, что этот вопрос равносилен вопросу о том, расположена ли точка (I во внутреннем полупространстве каждой ограничивающей полигон Р прямой. Для каждой ограничивающей прямой £. от нас требуется только проверить, составляет ли вектор 0, - Р1 с внешней нормалью угол больше 90°. Другими словами"opengl1_284.html">⇐ Предыдущая| |Следующая ⇒