Сначала каждый отрезок рисуется полностью красным цветом, а затем та его часть, которая расположена внутри полигона, окрашивается в синий цвет.
Тематическое задание 4.6. Отсечение полигона границами выпуклого полигона: отсечение Сазерленда-Ходгмана Уровень сложности III.
До сих пор изучаемые нами алгоритмы отсечения отсекали отдельные отрезки прямых границами полигона. Однако когда производится отсечение полигона границами окна, этот полигон можно разбить в процессе отсечения на несколько других полигонов, как предложено на рис. 4.52, а. Возможно, этот
4.10. Тематические задания полигон требуется заполнить цветом или узором, а это означает, что этот узор должен окрашивать каждый из отсеченных фрагментов, как показано на рис. 4.52,6. Следовательно, алгоритм отсечения должен рисовать ребра аЬ, ей и т. д. и должен сформировать новый полигон (или несколько полигонов) из исходного полигона. Важно, что алгоритм не сохраняет ненужные ребра, такие как Ьс, в качестве элементов нового полигона, и такие ребра не будут нарисованы, так как в действительности они должны быть невидимыми.
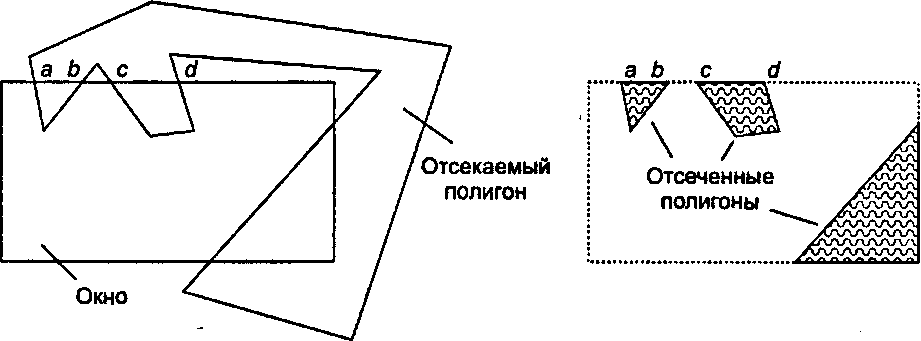
а б Рис. 4.52. Отсечение полигона границами полигона Назовем тот полигон, который подлежит отсечению, отсекаемым (subject) полигоном 5. Тот полигон, границами которого отсекается полигон 5, будем называть отсекающим (clip) полигоном С. Как же нам произвести отсечение полигона 5, представленного списком вершин, границами полигона С, чтобы создать совокупность списков вершин, правильно представляющую множество отсеченных полигонов?
Здесь мы используем алгоритм отсечения Сазерленда-Ходгмана, который достаточно прост и отсекает любой полигон (выпуклый или нет) границами выпуклого отсекающего полигона. Этот алгоритм может оставлять ненужные ребра, которые в дальнейшем необходимо удалить.
В силу того, что может возникнуть множество различных вариантов, нам необходим организованный метод слежения за ходом процесса отсечения. В алгоритме Сазерленда-Ходгмана используется метод «разделяй и властвуй»: сложная задача разбивается на несколько простых. Этот метод основан на подходе Сайруса-Бека, однако в данном случае он должен работать со списком вершин, представляющих полигон, а не просто с парой вершин.
