О Пересечение (intersection): An В" {все точки в обоих множествах А и В).

О Объединение (union): А и В = {все точки в А или в В или в них обоих}.

О Вычитание (разность, difference): А - В - {все точки в А, но не в В}.

Аналогичное определение дается для вычитания В - А.

Примеры этих множеств показаны на рис. 4.58.

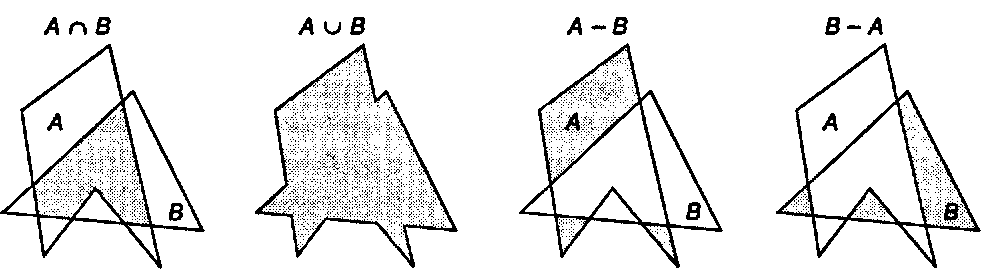
Рис. 4.58. Полигоны, образованные в результате булевских операций над полигонами

4.10. Тематические задания Нетрудно приспособить метод Вейлера-Азертона, который уже выполняет пересечение, к выполнению операций объединения и разности полигонов А и В.

1. Вычисление объединения полигонов А и В. Для настройки этой операции будем обходить полигон А в прямом направлении до тех пор, пока не обнаружим выходную точку пересечения - такую точку, при переходе через которую полигон А из внутренней области полигона В становится его наружной областью. Мы записываем эту точку пересечения и продолжаем обходить А до обнаружения следующего его пересечения с В. Затем мы переходим к обходу В в его прямом направлении. При каждом последующем пересечении мы записываем вершину и переходим к обходу другого полигона в его прямом направлении. Вернувшись к исходной вершине, ищем другие выходные пересечения, в которых мы еще не побывали.

2. Вычисление разности полигонов АиВ (внешнее отсечение - outside clipping). Поскольку нахождение пересечения двух полигонов дает в результате отсечение одного из них границами другого, операция вычитания «заслоняет» один полигон другим. Это означает, что разность двух полигонов SUBJ - CLIP состоит из тех частей полигона SUBJ, которые располагаются вне CLIP. Не подлежит рисованию ни одна часть SUBJ, расположенная внутри границы CLIP, так что область, заданная полигоном CLIP, надежно защищена, или заслонена.

Для реализации этого алгоритма мы будем обходить полигон А до обнаружения его входной точки пересечения с полигоном В. Затем переходим к В и обходим в его обратном направлении - так, чтобы внутренняя часть В оставалась слева. После достижения следующей точки пересечения снова перескакиваем на А. При достижении каждой точки пересечения мы перескакиваем на другой полигон и всегда обходим полигон А в прямом направлении, а В - в обратном. Ряд примеров по образованию объединения и разности двух полигонов приведен на рис. 4.59. Применение операций объединения и вычитания формирует следующие полигоны"opengl1_293.html">⇐ Предыдущая| |Следующая ⇒