Преобразования объектов в сравнении с преобразованиями координат
Можно рассматривать преобразование с двух сторон: преобразование объекта (object transformation) и преобразование координат (coordinate transformation). При преобразовании объекта координаты каждой его точки изменяются в соответствии с некоторыми законами, а соответствующая система координат остается неизменной. При преобразовании координат старая система координат преобразуется в новую, и все точки объекта получают представление в этой новой системе координат. Эти два подхода тесно связаны между собой, каждый из них имеет свои преимущества, однако реализуются они по-разному. Вначале мы рассмотрим основные идеи в терминах преобразований объекта, а затем приложим их к преобразованиям координат.
5.2.1. Преобразование точек и объектов Рассмотрим сначала общую идею преобразования, а затем частный случай аффинного преобразования.
Любое преобразование переводит каждую точку Р в пространстве (двумерном или трехмерном) в новую точку Q согласно заданной формуле или алгоритму. На рис. 5.8 показаны примеры для двух и трех измерений.
Как показано на рисунке, произвольная точка Р на плоскости отображена (is mapped) в другую точку Q. Тогда мы говорим, что точка Q является образом (image) точки Р при отображении Т. На рис. 5.8, а показана двумерная точка Р, отображаемая в новую точку Q, на рис. 5.8, б показана трехмерная точка Р, отображаемая в новую точку Q. Преобразование всего объекта осуществляется посредством преобразования каждой из его точек, причем для каждой точки используется, разумеется, та же самая функция Г( ). Можно отображать за один раз целые совокупности точек. Такой совокупностью могут быть все точки прямой или все точки окружности. Например, образ прямой L при преобразовании Гсостоит из образов всех отдельных точек прямой LK
1 Более строго: если 5 - множество точек, то его образ Г(5) является множеством всех точек Т(Р), где Р - некоторая точка из множества 5.
5.2. Введение в преобразования
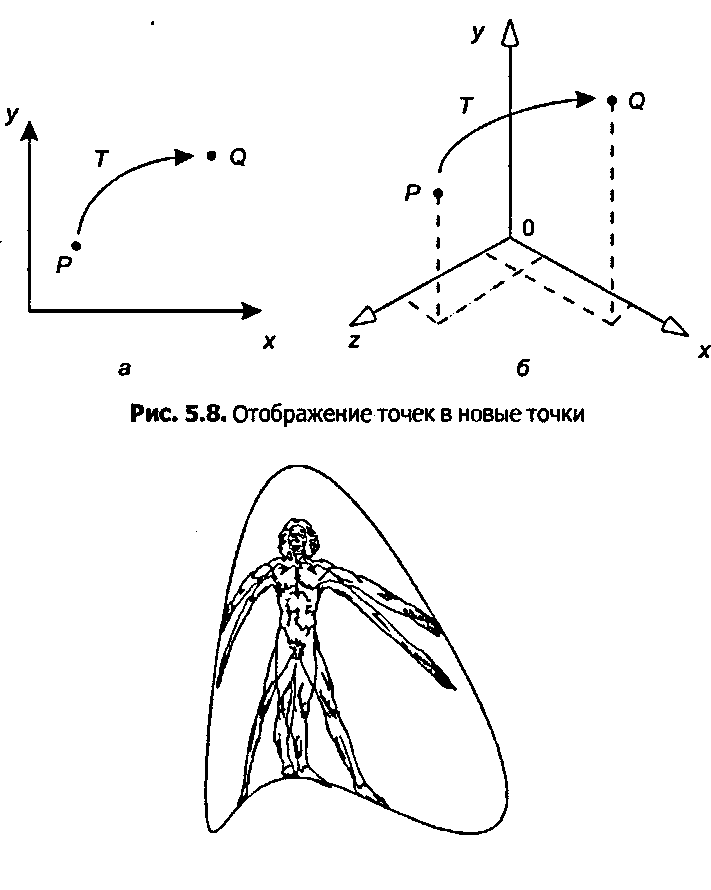
Рис. 5.9. Сложное преобразование фигуры
