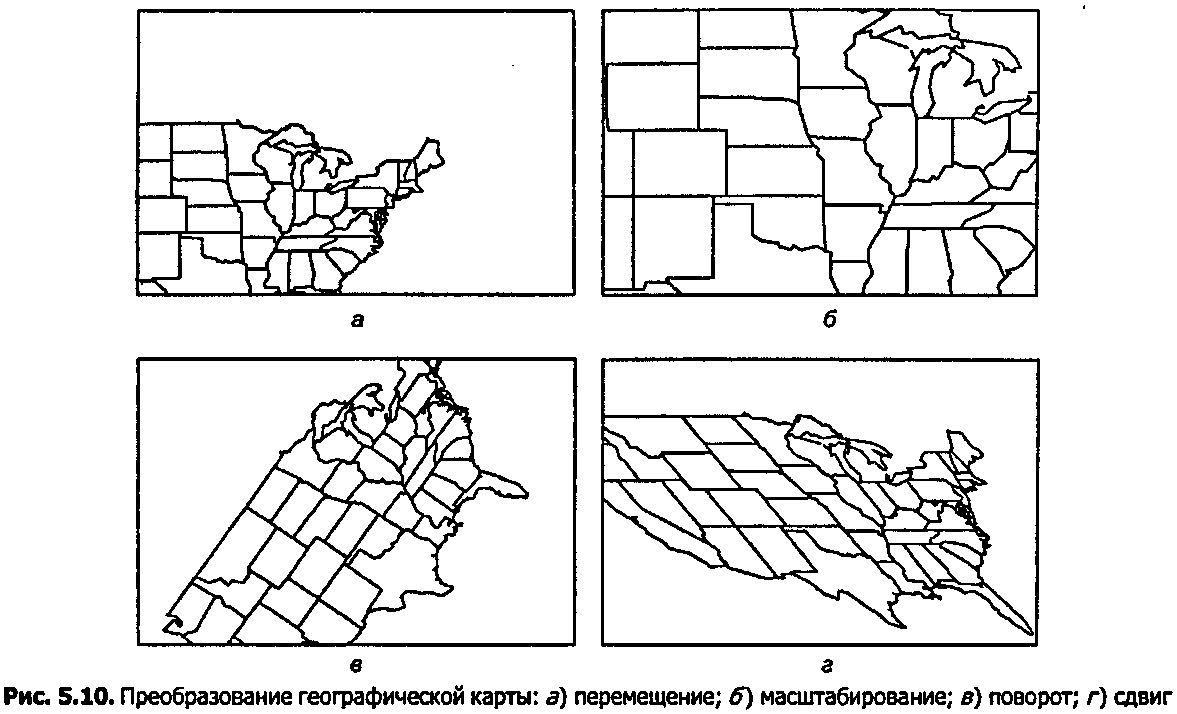
На рис. 5.10 показан пример действия каждого типа преобразований, примененного в отдельности.
Перемещение Часто требуется переместить изображение в другое положение на дисплее. Часть аффинного преобразования, отвечающая за перемещение, располагается в третьем столбце преобразующей матрицы:
(5.6)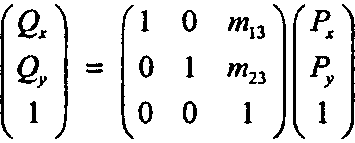
или просто
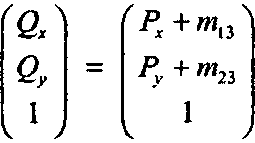
Тогда в обычных координатах имеем 0, - Р + <1, где с1 - (т1У яг23) - «вектор перемещения».
Если, например, вектор перемещения равен (2,3), то каждая точка будет перенесена в новую точку, которая на две единицы правее и на три единицы выше исходной точки. В этом случае точка (1, -5) преобразуется в точку (3, -2), а точка (0,0) - в точку (2,3).
Масштабирование Масштабирование изменяет размер изображения и использует два масштабных множителя - Бх и 5# для координат х и у соответственно: Тогда матрица для масштабирования в 5Х и 5у раз соответственно в координатных направлениях х и у имеет следующий простой вид:
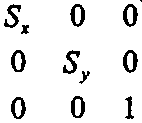
Более строго такой способ масштабирования называется масштабированием относительно начала отсчета (scaling about the origin), поскольку каждая точка Р передвигается в Sx раз дальше от начала отсчета в направлении х и в Sy раз дальше от начала отсчета в направлении у. Если масштабный множитель отрицателен, то происходит также отражение (reflection) относительно координатных осей. На рис. 5.11 показан пример, в котором масштабирование (Sx, Sy) = (-1,2) применено к совокупности точек. Каждая точка отражается относительно оси у и одновременно масштабируется в 2 раза в ^-направлении.
Существуют также «чистые» отражения, при которых каждый из масштабных множителей равен +1 или -1. Пример такого отражения: ПРх,Ру)-(-Рх,Ру)> (5.8)
в результате которого происходит зеркальное отражение картинки посредством «переворота» ее по горизонтали относительно оси у, причем каждое значение координаты х заменяется на -х. (Как выглядит матрица этого преобразования?)
5.2. Введение в преобразования Рис. 5.11. Масштабирование и отражение Если оба масштабных множителя одинаковы (Sx=* Sy= 5), то такое преобразование называется равномерным масштабированием (uniform scaling) или увеличением (magnification) относительно начала отсчета, с кратностью увеличения |5|. Если 5 отрицательно, то происходят отражения относительно обеих осей. Точка отодвигается от начала отсчета в |5| раз дальше. Если |5| < 1, то точки будут придвигаться ближе к началу отсчета, что приводит к уменьшению (или «антиувеличению» - «demagnification») изображения. Если же масштабные множители различны, то такое масштабирование называется дифференцированным масштабированием (differential scaling).
