Пример 5.2.9. Поворот вокруг точки Преобразование, которое уже изучалось в примере 5.2.5, состоит из поворота на 30° относительно точки (-2, 3) и имеет следующую матрицу:

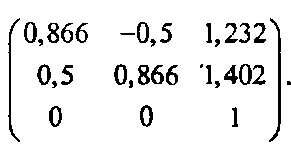
Как показано на рис. 5.22, б, в этом случае координатный фрейм преобразуется в новый координатный фрейм с началом отсчета (1,232,1,402,1) и координатными осями, задаваемыми векторами (0,866, 0,5,0) и (-0,5,0,866,0). Отметим, что эти оси остаются перпендикулярными, поскольку осуществлялся только поворот.

Относительные пропорции сохраняются Аффинные преобразования имеют еще одно полезное свойство. Рассмотрим точку Р, расположенную на части г расстояния между двумя заданными точками А и В, как показано на рис. 5.23. Применим аффинное преобразование Т( ) к точкам А, В и Р. Мы утверждаем, что преобразованная точка Т(Р) также располагается на той же части £ расстояния между образами точек Т(А) и Т(В). Это нетрудно показать. (См. упражнения в конце данного раздела.)

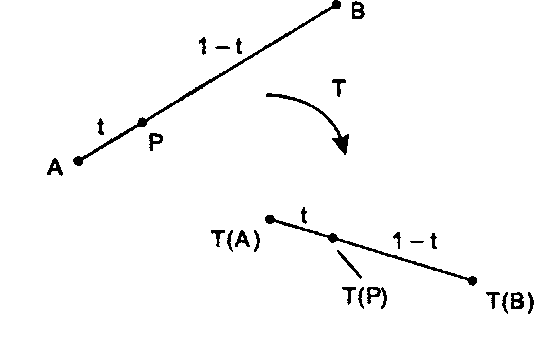
Рис. 5.23. Относительные пропорции сохраняются В частности, середины отрезков преобразуются также в середины отрезков. Это свойство приводит к замечательному геометрическому результату"opengl1_318.html">⇐ Предыдущая| |Следующая ⇒