М=М2М1. . (5.30)

Таким способом можно компоновать любое количество аффинных преобразований, и в результате получится одна матрица, представляющая суммарное преобразование.

Преобразования объектов

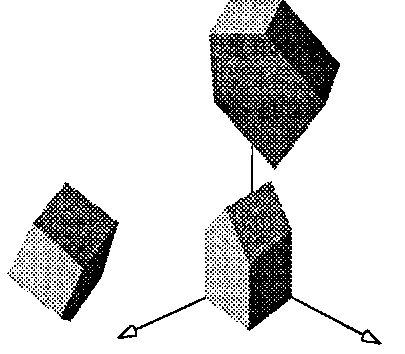
Рис. 5.27. Компонование трехмерных аффинных преобразований На рис. 5.27 показан пример, в котором сарай сначала преобразуется с помощью некоторой матрицы М,, после чего преобразованный сарай снова преобразуется с использованием матрицы М2. Результат совпадает с тем, который получится при одном преобразовании этого сарая с матрицей M2MV

5.3.3. Комбинирование поворотов Результаты! Ну, конечно, я получил кучу результатов. Теперь я знаю тысячи вещей, которые не будут работать.

Томас А. Эдисон (Thomas A. Edison)

Одно из самых важных различий между двумерными и трехмерными преобразованиями заключается в способе сложения поворотов. В двумерном случае два поворота, например кф{) и Я(Р2), при сложении дают /?(Р, + Р2), причем порядок, в котором складываются эти повороты, значения не имеет. В случае трех измерений дело обстоит намного сложнее, поскольку повороты могут происходить вокруг различных осей. Порядок, в котором осуществляются два поворота вокруг различных осей, имеет значение"opengl1_325.html">⇐ Предыдущая| |Следующая ⇒