О При аффинных преобразованиях прямые линии и плоскости сохраняются. «Прямизна» сохраняется: образ T(L) прямой L в трехмерном пространстве также является прямой; образ Т( W) плоскости W в трехмерном пространстве также является плоскостью.
О Сохраняется параллельность прямых и плоскостей. Если W\iZ- параллельные прямые (или плоскости), то их образы T(W) и T(Z) также параллельны.
О Столбцы матрицы показывают преобразованный координатный фрейм. Если столбцами матрицы М являются векторы т,, т2, т3 и точка т4, то преобразование отображает фрейм из (i, j, k, f}) в (m,, m2, m3, m4).
О Относительные пропорции сохраняются. Если Р находится на части /расстояния от точки А до точки В, то Т(Р) находится на части/расстояния от точки Т(А) до точки Т(В).
Преобразования объектов
О Влияние преобразований на объемы объектов. Если трехмерный объект И имеет объем V, то его образ Т(Р) имеет объем |<1е1Л/| V, где |с1е1М| - абсолютная величина определителя матрицы М.
О Каждое аффинное преобразование состоит из элементарных операций. Трехмерное аффинное преобразование может быть разложено на элементарные преобразования, причем несколькими способами.
5.4. Изменения систем координат
Можно рассматривать аффинные преобразования с другой точки зрения. В случае моделирования сцен это во многих отношениях более естественный подход. Вместо того чтобы рассматривать аффинное преобразование как создание новой точки в неизменной системе координат, рассмотрим его как создание новой системы координат, в которой нужно отобразить точки.
Несколько слов об обозначениях. Для того чтобы запись лучше помещалась на странице книги, мы иногда будем писать (Р, Р, 1)г вместо
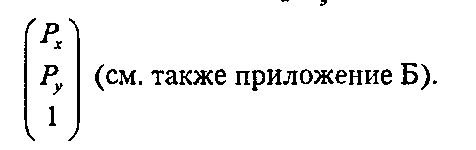
Надстрочное Т означает транспонировать (transpose), так что мы просто записываем вектор-столбец в виде транспонированного вектора-строки.
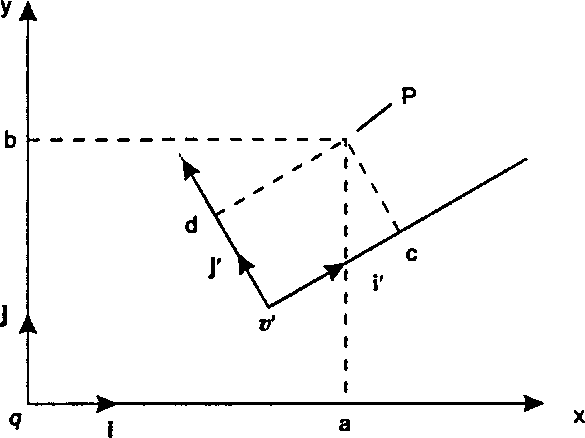
Рис. 5.31. Преобразование координатного фрейма Допустим далее, что у нас имеется двумерный координатный фрейм № 1, как показано на рис. 5.31, с началом отсчета V и осями і ну Пусть, далее, мы имеем аффинное преобразование Г(.), представленное матрицей М. Тогда Т(.) преобразует координатный фрейм № 1 в координатный фрейм № 2 с новым началом отсчета т}' = Г(т))и новыми осями і' = 7(1) и У = Т(}).
