5.5. Использование аффинных преобразований в программах

Купить рыбу с доставкой на дом в спб. Купить рыбу с доставкой на дом спб.

Мы хотим узнать, как теория аффинных преобразований применяется в программах при осуществлении масштабирования, поворота и перемещения графических объектов. Мы также исследуем, как это делается при использовании OpenGL. Сначала мы разберем двумерные примеры, так как они более наглядны. Затем мы перейдем к трехмерным примерам.

На данном этапе предположим, что мы имеем подпрограмму houseO, которая рисует домик № 1 на рис. 5.34. Пусть вместо этого домика вы хотите нарисовать домик № 2, повернутый на -30° и затем перемещенный на (32, 25). Подобная ситуация встречается очень часто: имеется заданный объект подходящего размера и расположения, однако нам нужно нарисовать его (и, возможно, много раз) с другими размерами, ориентацией и расположением.

Как уже рассматривалось в главе 3, подпрограмма house ( ) будет рисовать различные ломаные линии этой фигуры (домика). Если бы эта подпрограмма была написана на «голом» OpenGL, то она могла бы состоять из большого числа кусков такого вида:

glBegin(GL_LINES):
glVertex2d(V[0].x. V[0].y):
glVertex2d(V[l].x. V[l].y):
glVertex2d(V[2].x. V[2].y):

// the remaining points // остальные точки-glEndO:

Преобразования объектов

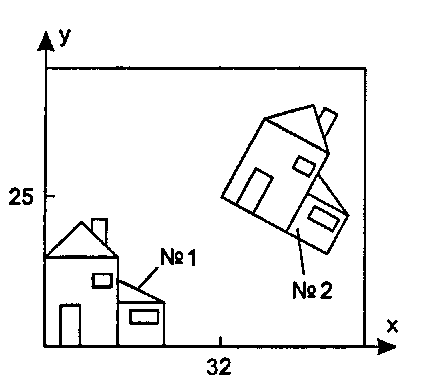
Рис. 5.34. Рисование домика с поворотом и перемещением Данный код мог бы использовать некоторый массив точек V[]. Если использовать класс Canvas, рассмотренный в главе 3 (а также глобальный объект класса Canvas cvs), то программа будет содержать многократные вызовы функций moveToO и lineToO такого вида"opengl1_335.html">⇐ Предыдущая| |Следующая ⇒