1) масштабирование с множителем 5,
2) поворот на угол А,
3) перемещение на (фс, йу), выполняемых именно в этом порядке. Список всех вентилей схемы хранится вместе с параметрами преобразований для каждого из них.
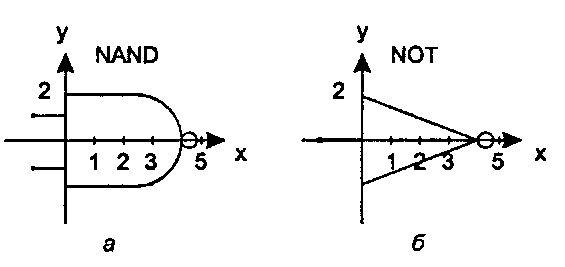
Рис 5.45. Каждый тип вентиля определяется в своей собственной системе координат
Всякий раз, когда рисунок должен быть обновлен, каждый экземпляр рисуется поочередно с применением соответствующего преобразования моделирования. Код этого обновления выглядит примерно так"opengl1_346.html">⇐ Предыдущая| |Следующая ⇒
